自动搬运

查看原文

来自洛谷，原作者为

	Supor__Shoep AFO | 耳畔之际，恋之回音。 | 你的她，青春永驻

搬运于2025-08-24 22:57:41，当前版本为作者最后更新于2024-05-04 16:46:30，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

就我觉得 T3 比 T4 简单吗QAQ

首先有一个非常常规的思路：枚举每一个数，求出其作为最大值的区间个数。这道题也是如此。

如果最终的序列 $a$ 长度够小，那么我们可以利用单调栈得出每一个数 $a_i$ 向前和向后的第一个 $>a_i$ 的数 $a_{l_i}$ 和 $a_{r_i}$，如果找不到则分别为 $0,|a|+1$，那么 $a_i$ 作为最大值的区间就有 $(i-l_i)(r_i-i)$ 个。

但是需要注意，有的区间是会被算重的，比如 $a=\{1,2,1,2\}$，两个 $2$ 分别计算得到的区间都包含 $[2,4],[1,4]$。这个时候考虑更改 $l_i$ 的定义为向前找到的第一个 $≥a_i$ 的数的下标，如果找不到则为 $|a|+1$，计算方式仍然是 $(i-l_i)(r_i-i)$。这样就可以保证不会重复计算了，原因显然，因此把它当成一个 Trick 掌握就行了。

但是出题人非常可爱啊！这个 $a$ 的长度可以达到 $10^{15}$，不可能直接计算。但是 $n$ 的范围倒是很合理。这就说明我们要找到 $a$ 序列的计算规律。

我们将 $a$ 视为 $n$ 个形如 $\{1,2,\dots,b_i-1,b_i\}$ 的子段前后拼接得到的序列，记 $s_{i,j}$ 表示第 $i$ 个子段中的第 $j$ 个数在 $a$ 中的下标。

先考虑 $s_{i,b_i}$ 的代价该怎么计算。由于各个子段的单调性，我们可以知道其向前能够找到的第一个 $≥b_i$ 的数的下标一定是 $s_{j,b_j}$（$j<i$），向后能够找到的第一个 $> b_i$ 的数的下标一定是 $s_{k,b_i+1}$（$i<k$，注意是 $b_i$ 而不是 $b_k$）。可以发现 $b_j$ 是 $b_i$ 向前第一个大于等于它的数，$b_k$ 是 $b_i$ 向后第一个大于它的数。可以通过这个结论，利用单调栈找到 $j,k$。我们找到这两个 $j,k$ 记为 $L(i),R(i)$（如果不存在满足条件的 $j$ 或 $k$，则分别变为 $0,n+1$），则 $s_{i,b_i}$ 的区间个数就是 $(s_{i,b_i}-s_{L(i),b_{L(i)}})(s_{R(i),b_{i}+1}-s_{i,b_i})$，可以利用 $b_i$ 的前缀和解决。

我们记 $sum_i=\sum _{j=1}^ib_j$，那么：

$$(s_{i,b_i}-s_{L(i),b_{L(i)}})(s_{R(i),b_{i}+1}-s_{i,b_i})=(sum_i-sum_{L(i)})(sum_{R(i)-1}-sum_i+1+[R(i)\leq n]) $$

每一个子段的顶点值我们就算完了，我们考虑将这种做法拓展到其它数上面。其实我们可以利用图像去思考：

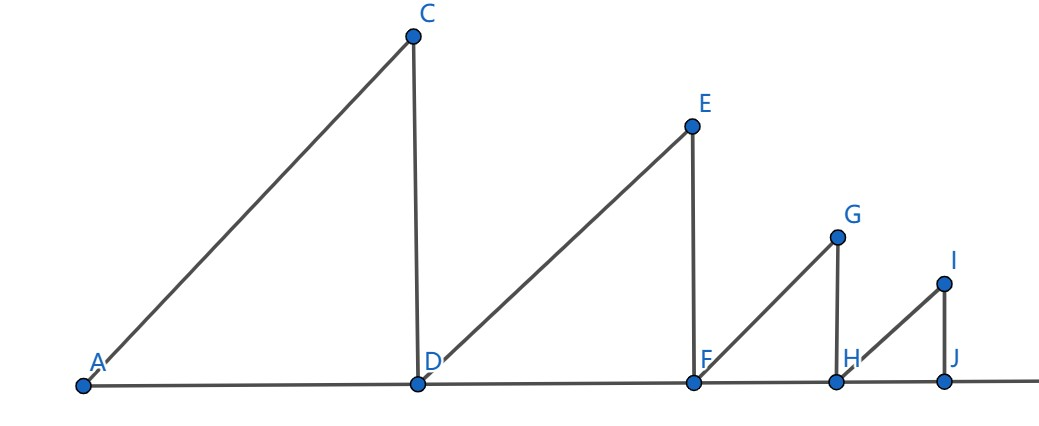
我们知道对于每一个数，要去找前面和后面比自己大的，由于除了顶点以外，每个数的后面都有一个比自己大一的数，所以右侧比较好找。而对于左侧，我们结合上图去思考，不难发现最终形成的 $a$ 序列就是若干个等腰直角三角形排在一起，那么每个数作为最大值的区间可以延展到的左端点一定是在 $s_{k,b_k}$ 的位置。因此我们像之前那样用一个单调栈就行了。

但是对于每个数都用单调栈的话显然会寄。

我们可以找一下规律：

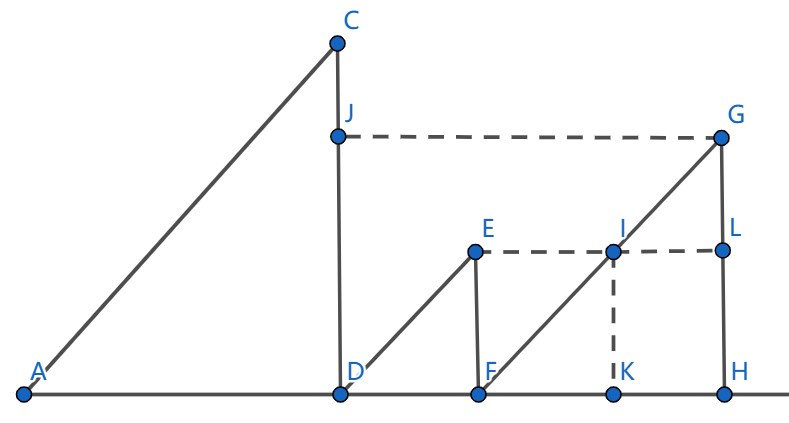
考虑对第 $3$ 个子段的每个元素的答案进行统计，我们发现 $IK$ 这一段对应过去的线段是 $EF$，这说明 $1\leq j\leq |IK|$ 的元素 $s_{3,j}$ 可以向左延伸的最远点都是 $F$，即 $s_{2,b_2}$。而 $GL$ 对应过去是 $CD$ 的一个子线段，这说明 $|IK|<j\leq |GH|$ 的元素 $s_{3,j}$ 向左延伸的最远点都是 $s_{1,b_1}$。这启示我们将每一个子段中的元素分成若干个子部分进行处理，并且要保证每个部分的 $s_{i,j}$ 对应的左侧端点是相同的。

于是我们用单调栈去储存 $b_i$，维护一个单调递减的子序列的下标。当我们要处理第 $i$ 个子段时，我们就在栈中从后往前遍历，设当前遍历的元素为 $p$，上一个遍历的元素是 $q$，那么我们就将 $[s_{i,b_q+1},s_{i,b_p}]$ 的答案进行加和，下文令 $t=sum_{i-1}-sum_p+b_q$，$m=b_p-b_q$，则：

$$\begin{aligned} \sum _{j=b_q+1}^{b_p}j(s_{i,j}-s_{p,b_p})&=\sum _{j=b_q+1}^{b_p}j(sum_{i-1}-sum_p+j)\\ &=\sum _{j=1}^{m}(b_q+j)(sum_{i-1}-sum_p+b_q+j)\\ &=mb_qt+\dfrac{m(b_q+t)(m+1)}{2}+\dfrac{m(m+1)(2m+1)}{6} \end{aligned} $$

这样就可以 $O(1)$ 计算这一段的答案之和了。

根据单调栈的性质，可以推断 $n$ 个子段分成的子部分的个数和是 $O(n)$ 级别的，可以跑过。

最后就是一些细节问题了，放代码：

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN=1e6+5;
const int MOD=998244353;
int n,a[MAXN];
stack<int> stk;
int res;
int L[MAXN],R[MAXN];
int sum[MAXN];
int qpow(int x,int y)
{
	int res=1;
	while(y)
	{
		if(y&1)	res=1ll*res*x%MOD;
		x=1ll*x*x%MOD;
		y>>=1;
	}
	return res;
}
int solve(int x,int y,int z){ return (1ll*x*y%MOD*z%MOD+1ll*(x+y)%MOD*(1ll*(z+1)*z/2%MOD)%MOD+1ll*z*(z+1)%MOD*(2*z+1)%MOD*qpow(6,MOD-2)%MOD)%MOD; }
signed main()
{
	cin>>n;
	for(int i=1;i<=n;i++)	cin>>a[i],sum[i]=sum[i-1]+a[i],sum[i]%=MOD;
	a[n+1]=a[n];
	for(int i=1;i<=n;i++)
	{
		while(!stk.empty()&&a[stk.top()]<a[i])	R[stk.top()]=i,stk.pop();
		if(!stk.empty())	L[i]=stk.top();
		stk.push(i);
	}
	while(!stk.empty())	R[stk.top()]=n+1,stk.pop();
	for(int i=1;i<=n;i++)	res+=1ll*a[i]*(sum[i]-sum[L[i]]+MOD)%MOD*(sum[R[i]-1]-sum[i]+1+(R[i]<=n)*a[i]+MOD)%MOD,res%=MOD;
	while(!stk.empty())	stk.pop();
	stk.push(0),a[0]=1e9;
	for(int i=1;i<=n;i++)
	{
		int lst=0;
		while(!stk.empty()&&a[stk.top()]<=a[i]-1)	res+=solve(sum[i-1]-sum[stk.top()]+lst,lst,a[stk.top()]-lst),lst=a[stk.top()],stk.pop();
		if(lst!=a[i]-1)	res+=solve(sum[i-1]-sum[stk.top()]+lst,lst,a[i]-lst-1),res%=MOD;
		while(!stk.empty()&&a[stk.top()]==a[i])	stk.pop();
		stk.push(i);
	}
	cout<<res;
	return 0;
}