1 条题解
-
0
自动搬运
来自洛谷,原作者为

spfa_
这个什么很懒,家伙也没有留下搬运于
2025-08-24 22:57:36,当前版本为作者最后更新于2024-05-07 17:13:56,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
才爆了五个标,太弱了认真分析语句的性质,得到:
-
只增不减,所以要计算的是增量
-
只减不增
-
跳转语句等价于
do-while,所以if语句本质上是实现不了的
那么如何实现任意次数次的循环呢?我们可以将一个变量变为想要次数的相反数,然后另外一个置 ,如何变量不等则一直减 ,就能实现循环了。对于多重循环只需嵌套一下即可。
那么通过循环就能实现一些简单的加,乘操作了。
task 1
,循环 次加一即可。
3 dec 1 new 2 ifneq 1 3 goto 1task 2
,从 循环到 即可。
9 dec 1 dec 1 dec 1 assign 2 1 dec 2 new 3 iftry 2 goto 5 dec 1 ifneq 1 4 goto 4task 3
,很直接的想法是构造出 次循环,变成相反数变成 , 可以视为 ,循环即可。
35 dec 2 dec 2 dec 2 dec 2 dec 2 dec 2 dec 2 dec 2 dec 2 dec 2 dec 2 dec 2 dec 2 dec 2 dec 2 dec 2 dec 2 dec 2 dec 2 dec 2 dec 2 dec 2 dec 2 dec 2 assign 3 2 dec 3 dec 4 assign 5 6 dec 5 dec 1 ifneq 5 3 goto 29 ifneq 4 2 goto 27 dec 6 new 8 ifneq 1 6 goto 33task 4
直接加一即可。
1 new 1task 5
。
10 assign 2 1 dec 2 dec 2 new 4 dec 1 assign 3 2 dec 3 new 4 ifneq 3 5 goto 7 iftry 1 goto 5task 6
。
24 dec 2 dec 2 dec 2 dec 2 dec 2 dec 2 dec 2 dec 2 dec 2 dec 2 dec 3 dec 3 dec 4 assign 5 8 dec 5 assign 6 8 dec 6 assign 7 8 dec 7 new 9 ifneq 7 2 goto 19 ifneq 6 2 goto 17 ifneq 5 2 goto 15 ifneq 3 4 goto 13task 7
考虑倍增。将 一直减去 的幂次,若大于等于 则倍增,次数加一。
13 assign 2 1 dec 3 dec 3 dec 2 dec 2 new 7 assign 4 3 assign 5 6 dec 5 dec 3 dec 2 ifneq 5 4 goto 9 iftry 2 goto 6task 8
考虑将 一直减 直到 ,那么 只会为 其中一种。而我们需要做的是将 的情况加 , 的情况加 。用一个初始为 的变量,减 并判断是否相等,相等再执行一遍加 操作。
6 dec 1 dec 1 iftry 1 goto 1 dec 2 new 3 ifeq 1 2 goto 4task 9
。
类似 task 8 的方法我们可以对 一直减 ,但是这里的处理方法有点不同。这里我将 的情况变为 的情况,然后有 的情况,需要增加的数分别为 。对于任意数先
new两次,然后减 。如果等于 则跳回第二个new,如果等于 跳回第一个new。18 dec 1 dec 1 dec 1 dec 1 assign 2 1 dec 2 iftry 2 goto 1 dec 3 dec 3 assign 4 3 dec 4 dec 4 new 5 new 5 dec 1 dec 1 ifeq 1 4 goto 14 ifeq 1 3 goto 13task 10
这里我用了点
奇淫技巧。思路是尽可能的构造一个一次函数,使得满足条件。然后玩弄半天后发现 最佳,似乎没有更好的了。下面是函数图像: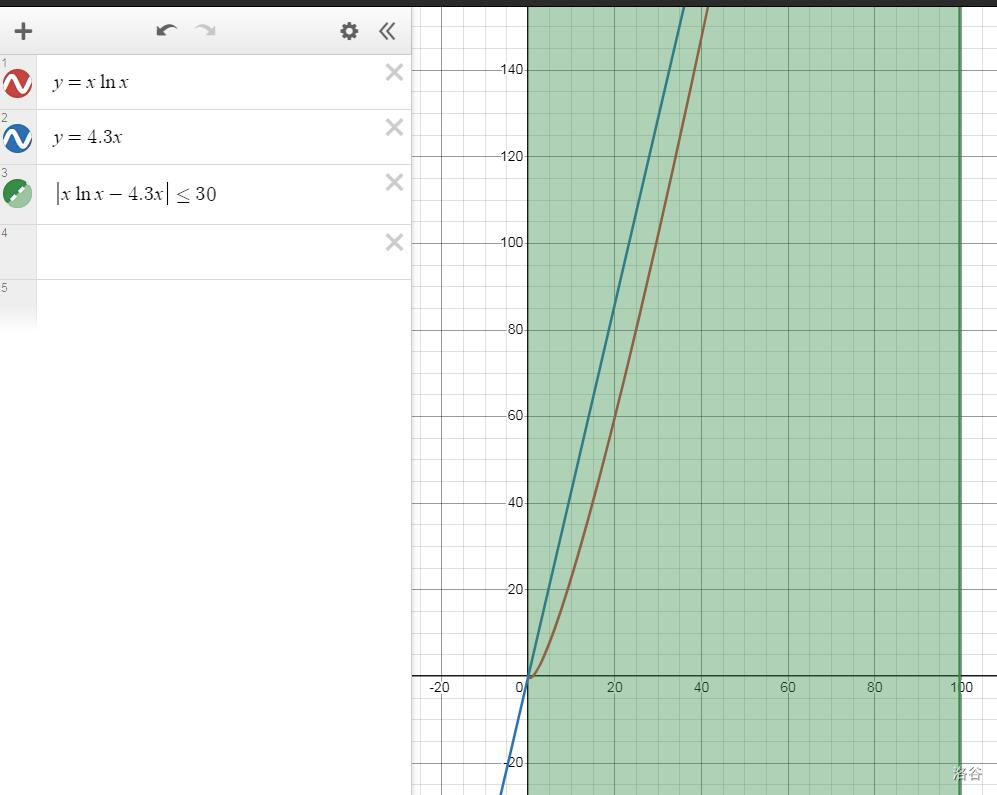
然后如何凑出 呢? 部分好搞,而 部分则可以看成 ,这个只需长度为 ,步长为 的循环即可,那么就解决了。
11 assign 2 1 dec 1 new 4 new 4 new 4 ifneq 1 3 goto 2 dec 2 dec 2 dec 2 new 4 iftry 2 goto 7 -
- 1
信息
- ID
- 9764
- 时间
- 3000ms
- 内存
- 512MiB
- 难度
- 7
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
