自动搬运

查看原文

来自洛谷，原作者为

	int08 学生 Div.1 rk 900||Day after day after day we fly, past the moon and the sun and we don't know why...

搬运于2025-08-24 22:57:14，当前版本为作者最后更新于2024-04-20 22:56:59，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

前言

我们一场模拟赛的题，结果原题是新鲜出炉的。

小弟不才，感觉这题是做过的题中几乎最复杂的了。

既然搞懂了，就来写一发题解吧。

（题外话：目前最优解，我的常数真是小小又大大啊）

"Up and down,glowin' round..."

Solution

1、一个经典的 Trick

直接模拟每一种情况显然不可取，考虑计算每一条的贡献。

假设对于第 $i$ 条，一共有 $x_i$ 条线段能在开了水龙头后流到它（包括它自己，故 $x_i \ge 1$）。

那么容易发现，这个位置的水龙头要打开，当且仅当它是这 $x_i$ 条中排第一个的。

这个概率在全排列下为 $\frac{1}{x_i}$，容易发现其他的线段对这一条贡献无影响，故答案为 $\sum_{i=1}^{n}x_i$。

现在我们只需要求出每一条能被多少条流到即可。

2、模拟运行，得出结论

首先按照高度从小到大排序。（本题中已经排好）

发现第 $i$ 条（之后记为 $a_i$）可以直接流到 $a_j$（$i>j$）的条件是如下之一：

1. $a_i$ 左右完全在 $a_j$ 中间。

2. $a_i$ 覆盖了 $a_j$ 的某一个端点。（下文将这种情况称 $a_i$ 为 $a_j$ 的左/右祖先）

但本题可不止直接流，间接流到（$a_i$ 流 $a_j$，$a_j$ 流 $a_k$）这种也算。

经过想象和模拟，我们可以猜测能流到它的区域的两端大概是不断从左/右祖先一次一次流下来，而中间的部分都可以。

但是还有一种情况，如果 $a_i$ 完全覆盖 $a_j$ 以及它的所有左右祖先，那么 $a_i$ 上面的所有线段都不可能流到 $a_j$ 了，我们可以称 $a_i$ 支配 $a_j$。

于是能流到的部分就是它不断向左右祖先去，直到被支配它的线段挡住为止。

如下图所示：

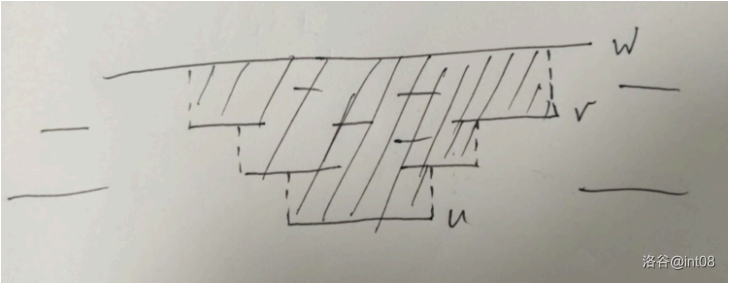
现在依次出现四个问题在我们面前，下文一一解释。

"...I saw somehow you know..."

3、解决四个问题

找到每条线段的左右祖先

由于一条线段左祖先是覆盖它的左端点的线段中高度最低（且大于它本身）的，于是从大到小扫描并使用线段树区间推平单点查询，这是简单的。

计算阴影内的线段个数

阴影部分看似是不规则的，但是我们可以用前缀相减的方式。

就像这样：

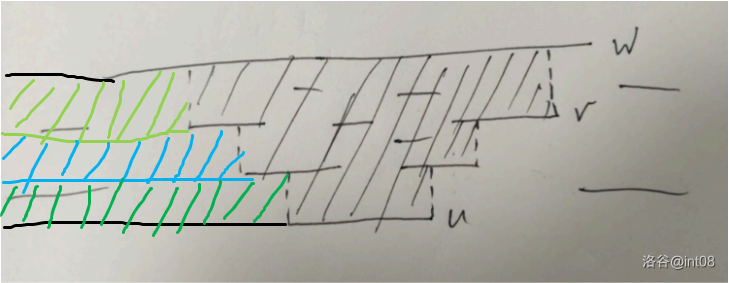
答案就是所有向右祖先跳的前缀减去所有向左祖先跳的前缀。

现在只需计算每个线段向它的祖先跳的这个 $\text{3-side}$ 内的线段个数，等价于数右端点个数。

经典二维数点，扫描线配合树状数组搞定。

找到支配线段

为了使得每条线段都有支配线段，我们在最顶上加一条最大的线段，但是这并不影响下面的答案。

现在每条线段都被它上面的某一条支配，这形成了一棵树。

而每条线段的支配线段，就是它的左右祖先在支配树上的 $\text{LCA}$。

理由：要支配它得同时支配它的左右祖先，而且它左右祖先的所有祖先显然就是它的所有祖先。

而 $\text{LCA}$ 可以使用倍增解决，倍增也支持动态加点，无敌了。

将计算答案和找到支配线段合并

很显然你可以在计算 $\text{LCA}$ 时带权，但不只是带上本身答案这么简单。

因为左右端点的答案可能重叠。

所以对于每个点，我们应该分别记录它到支配点的左右轮廓对应的前缀和，这样合并方便，相减得出答案也不会算重。

事实上，以上内容说着简单，严谨性却有缺失，大家可以自己再思考，再证明，作为对这道题目的再利用。

AC code

代码有些难写，这题真的只有紫吗……

"...I might get down,you might not drown..."

"...You might just fly away."

#include<bits/stdc++.h>
#define N 508032
#define mod 1000000007
using namespace std;
long long qp(long long x,long long y)
{
	long long ans=1;
	for(long long i=1,j=x;i<=y;i*=2,j=j*j%mod) if(i&y) ans=ans*j%mod;
	return ans;
}
//bit
int bit[2*N],n;
void change(int x,int y)
{
	for(;x<=2*n;x+=x&-x) bit[x]+=y;
}
int ask(int x)
{
	int ans=0;
	for(;x;x-=x&-x) ans+=bit[x];
	return ans;
}
//sgt
struct tree{
	int l,r,ans;
}sgt[8*N];
#define mid ((sgt[o].l+sgt[o].r)>>1)
#define ls (o*2)
#define rs (o*2+1)
void build(int l,int r,int o)
{
	sgt[o].l=l,sgt[o].r=r;
	if(l==r) return;
	build(l,mid,ls);
	build(mid+1,r,rs);
}
void pushdown(int o)
{
	if(sgt[o].ans&&sgt[o].l!=sgt[o].r)
	{
		sgt[ls].ans=sgt[rs].ans=sgt[o].ans;
		sgt[o].ans=0;
	}
}
void change(int l,int r,int v,int o)
{
	pushdown(o);
	if(sgt[o].l>=l&&sgt[o].r<=r)
	{
		sgt[o].ans=v;
		return;
	}
	if(l<=mid) change(l,r,v,ls);
	if(r>mid) change(l,r,v,rs);
}
int ask(int x,int o)
{
	pushdown(o);
	if(sgt[o].l==sgt[o].r) return sgt[o].ans;
	if(x<=mid) return ask(x,ls);
	else return ask(x,rs);
}
//LCA
struct Lca{
	int lc,la,ra;
};
int d[N];
Lca p[N][23];
Lca lca(int a,int b)
{
	int lans=0,rans=0;
	for(int i=21;i>=0;i--)
		if(d[a]<=d[b]-(1<<i))
			rans+=p[b][i].ra,b=p[b][i].lc;
	for(int i=21;i>=0;i--)
		if(d[b]<=d[a]-(1<<i))
			lans+=p[a][i].la,a=p[a][i].lc;
	if(a==b) return {a,lans,rans};
	for(int i=21;i>=0;i--)
	{
		if(p[a][i].lc==p[b][i].lc) continue;
		else lans+=p[a][i].la,rans+=p[b][i].ra,a=p[a][i].lc,b=p[b][i].lc; 
	}
	return {p[a][0].lc,lans+p[a][0].la,rans+p[b][0].ra};
}
//segment
int l[N],r[N],bel[2*N],i,j,val[N];
int lf[N],rf[N],lv[N],rv[N];
struct smx{
	int id,x,k;
};
inline int read()
{
	int ret=0;
	char ch=getchar();
	while(!isdigit(ch))
		ch=getchar();
	while(isdigit(ch))
		ret=(ret<<3)+(ret<<1)+(ch^48),ch=getchar();
	return ret;
}
vector<smx> s[N];
signed main()
{
	n=read();
	for(i=1;i<=n;i++) l[i]=read(),r[i]=read(),bel[++l[i]]=bel[++r[i]]=i;
	n++;l[n]=1,r[n]=2*n;bel[l[n]]=bel[r[n]]=n;
	build(1,2*n,1),change(1,2*n,n,1);
	for(i=n-1;i>=1;i--)
		lf[i]=ask(l[i],1),rf[i]=ask(r[i],1),change(l[i],r[i],i,1),
		s[lf[i]].push_back({0,l[i],-1}),s[i].push_back({0,l[i],1}),
		s[rf[i]].push_back({1,r[i],-1}),s[i].push_back({1,r[i],1});
	for(i=n;i>=1;i--)
	{
		change(r[i],1);
		for(auto v:s[i])
		if(!v.id) lv[bel[v.x]]+=v.k*ask(v.x);
		else rv[bel[v.x]]+=v.k*ask(v.x);
	}
	for(i=n-1;i>=1;i--)
	{
		Lca repair=lca(lf[i],rf[i]);
		int fa=repair.lc;
		val[i]=repair.ra-repair.la-lv[i]+rv[i];
		d[i]=d[fa]+1;
		p[i][0]={fa,repair.la+lv[i],repair.ra+rv[i]};
		for(j=1;(1<<j)<=d[i];j++) p[i][j]={p[p[i][j-1].lc][j-1].lc,p[p[i][j-1].lc][j-1].la+p[i][j-1].la,p[p[i][j-1].lc][j-1].ra+p[i][j-1].ra};
	}
	long long ans=0;
	for(i=1;i<=n-1;i++) (ans+=qp(val[i],mod-2))%=mod;
	cout<<ans;
	return 0;
}

The End.