自动搬运

查看原文

来自洛谷，原作者为

	I_AM_CIMOTA I am trρ_hy

搬运于2025-08-24 22:57:05，当前版本为作者最后更新于2025-01-07 20:29:06，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

本题大致可以分为两个部分。

子任务 2

由于所有元素互不相同，那么 $f(i,j)$ 就等于 $j-i+1$ 了，此时选取区间中点一定是最优的。

于是枚举区间长度，每个长度的区间贡献都可以 $O(1)$ 求。

其余部分

根据数据范围猜做法。

注意到 $nm$ 最多只有 $80000\times600=48000000$，而且时限是 4s，于是可以考虑用 $O(nm)$ 或多一个 $\log$ 的算法求解。

怎样快速计算 $f(i,j)$ 呢？可以参考 HH的项链，比较经典所以这里就不讲了。

我们在求 $f(i,j)$ 的时候，是固定了一个右端点 $r$，然后转化为区间求和。那么对于一个 $r$，所有 $f(i,r)$ 相同的 $i$ 一定构成一个区间，而这样的区间一定是不超过 $m$ 个的（因为总颜色数只有 $m$ 种），于是我们可以维护 $O(m)$ 个断点。随着端点 $r$ 向右移动，这些断点要么向右移动，要么留在原位，那么所有断点的总移动量就是 $O(nm)$ 的。

那么加上树状数组维护区间和，移动端点花费的时间为 $O(nm\log n)$。

假设现在 $r$ 固定，我们定义 $pt_i$ 表示所有 $x\in(pt_{i+1},pt_i]$ 都满足 $f(x,r)=i$，其实也就是断点。

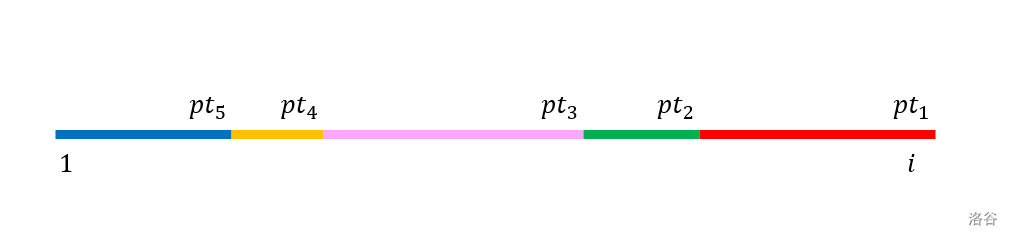
我们在回过头来观察原式：$\max_{1\le i\le k}\{i\times f(i,k)\}$，现在需要对于每个 $l\in[1,r]$ 求出这个值。

对于某一个 $l$，其最优决策点为 $pos$，那么就得让 $pos\times f(pos,r)$ 最大。显然，如果颜色数 $c=f(pos,r)$ 已经确定，那么我们一定会选 $pt_c$ 作为决策点，因为它的下标最大。于是，把所有可能的颜色数考虑进来，最优决策点一定就在 $pt_1,pt_2,\cdots,pt_m$ 这些断点中的某一个上。

现在，我们知道了每个 $l$ 的最优决策点一定是在某个断点处，那么我们考虑对于一个 $l$ 找到最优决策点。观察贡献的式子：

上式中 $pt_c-l+1$ 代表区间以 $l$ 作为左端点时 $pt_c$ 的下标，$c$ 就是颜色数 $f(pt_c,r)$。式子经过变形可得：

这个东西可以抽象为：一条斜率为 $l$ 并且经过点 $(c,pt_c\times c+c)$ 的直线在纵轴上的截距。于是可以对所有 $(c,pt_c\times c+c)$ 构建一个上凸壳，最优决策点一定在凸壳上。

那么对于一个确定的 $l$，我们可以二分求出最优决策点，统计答案。现在算答案时间复杂度达到了 $O(n^2\log m)$。

这个时间复杂度还是不够优秀，考虑优化。因为我们猜测的目标时间复杂度与 $nm$ 有关，于是想到直接枚举所有断点，看每个断点能成为哪些 $l$ 的最优决策点。

我们画一张图：

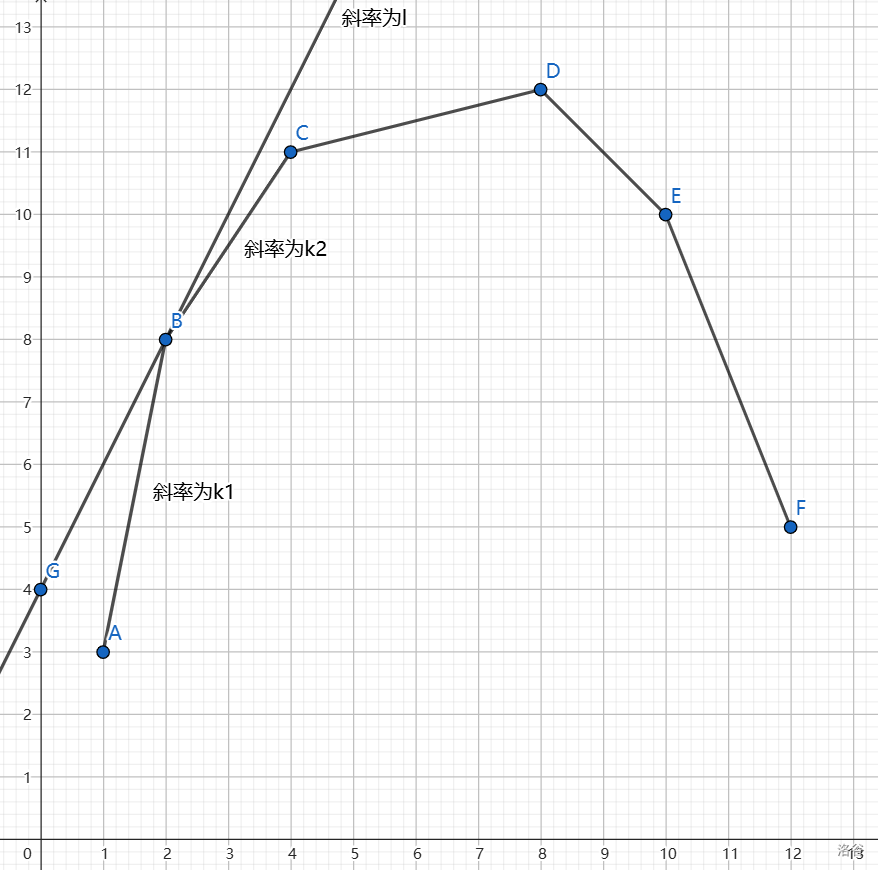
显然，如果 $B$ 要成为左端点 $l$ 的最优决策点，必须满足 $k_2\le l\le k_1$，这是一个连续的区间，于是可以用等差数列求和来统计贡献。这时候，算答案的时间复杂度就降到了 $O(nm)$。

与前面结合起来，复杂度瓶颈在于移动断点的 $O(nm\log n)$。

#include <bits/stdc++.h>
#define int long long
using namespace std;

const int N=1e5+5,Mod=998244353;
int n,m,ans,tot,a[N],pos[N],las[N],pt[N];
bool vis[N];

namespace BIT{//树状数组
    int t[N];
    void upd(int x,int add){for(;x<=n;x+=x&(-x))t[x]+=add;}
    int qry(int x){
        int res=0;
        for(;x;x-=x&(-x))res+=t[x];
        return res;
    }
    int qry(int l,int r){return qry(r)-qry(l-1);}
}
using namespace BIT;

namespace CONV{//凸壳
    int tp;
    struct Comp{
        int x,y;
    }p[N],st[N];
    struct Line{
        Comp P,Q;
        double k(){return 1.0*(Q.y-P.y)/(Q.x-P.x);}
    };
    void get_conv(){
        tp=0;
        st[++tp]=p[1];
        if(tot==1)return;
        st[++tp]=p[2];
        for(int i=3;i<=tot;i++){
            Line pre={st[tp-1],st[tp]},nw={st[tp],p[i]};
            while(pre.k()<nw.k()){
                tp--;
                if(tp==1)break;
                pre={st[tp-1],st[tp]},nw={st[tp],p[i]};
            }
            st[++tp]=p[i];
        }
    }
}
using namespace CONV;

signed main(){
    scanf("%lld",&n);
    for(int i=1;i<=n;i++){
        scanf("%lld",&a[i]);
        if(!vis[a[i]])m++,vis[a[i]]=1;
        las[i]=pos[a[i]];
        pos[a[i]]=i;
    }
    if(m<=800){//subtask1,3,4,5
        for(int i=1;i<=n;i++){
            if(las[i])upd(las[i],-1);
            upd(i,1);
            for(int j=1;j<=m;j++)while(qry(pt[j]+1,i)==j)pt[j]++;//移动断点
            tot=0;
            for(int j=1;j<=m;j++)if(pt[j])p[++tot]={j,pt[j]*j+j};
            get_conv();
            int lasR=0;//为了不重复统计，直接每次把左界设为上一次的右界加1
            for(int j=tp;j>=1;j--){
                int L=lasR+1,R=i;
                if(j>1){
                    Line A={st[j-1],st[j]};
                    R=min(R,(int)floor(A.k()));
                }
                if(j<tp){
                    Line A={st[j],st[j+1]};
                    L=max(L,(int)ceil(A.k()));
                }
                if(L>R)continue;
                ans+=-((L+R)*(R-L+1)/2)*st[j].x+(R-L+1)*st[j].y;
                ans=(ans%Mod+Mod)%Mod;
                lasR=R;
            }
        }
        printf("%lld\n",ans);
    }
    else{//subtask2
        for(int i=1;i<=n;i++){
            if(i&1)ans+=((i+1)/2)*((i+1)/2)%Mod*(n-i+1)%Mod;
            else ans+=(i/2)*(i/2+1)%Mod*(n-i+1)%Mod;
            ans%=Mod;
        }
        printf("%lld\n",ans);
    }
    return 0;
}