自动搬运

查看原文

来自洛谷，原作者为

	NaCly_Fish 北海虽赊，扶摇可接。

搬运于2025-08-24 22:56:56，当前版本为作者最后更新于2024-04-05 22:49:21，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

测试点 1（W）

W：Warm-up，即热身。

没有什么特殊性质，数据范围也比较小的一个测试点。这里也不需要什么特殊的优化算法，只需要设 $f_{u,S}$ 表示从 $u$ 节点出发的所有点权为 $S$ 的路径的答案，就可以得到 DP：

$$f_{u,S}=\sum_{(u,v)\in E}w(u,v)\times f_{v,S-w(u)} $$

其中 $w(u,v)$ 表示 $u\to v$ 的边权，$w(u)$ 表示 $u$ 节点的权值。直接计算即可，时间复杂度 $\mathcal O(mV)$。

测试点 2,3,4（K）

K：完全图。

在这里，给定的图都是完全图（$n^2$ 条边），且所有边的权值都相等，考虑这种情况下如何计数。由于这是个完全图，任意一个点权和为 $V$ 的节点序列都是合法的路径。可以枚举路径的长度 $k$，得到答案是：

$$\sum_{k\geq 1}q^{k-1}[x^V]\left( \sum_{i=1}^n x^{w(i)}\right)^k $$

其中 $q$ 表示边的权值，这个式子的意义也比较明显了（$k$ 个位置，每个位置都可以任选一个节点，保证点权和为 $V$ 即可）。化简一下就是

$$q^{-1}[x^V] \frac{1}{1-q\sum_{i=1}^nx^{w(i)}}$$

设 $W$ 是最大的点权，使用 FFT 优化的 LSB-first 算法，就能简单地做到 $\Theta(W \log W \log V)$ 的时间复杂度。足以解决测试点 $2,3$。如果使用矩阵快速幂，也能在可接受的时间内通过测试点 2。

对于测试点 $4$，$W$ 很大但递推系数非常稀疏，是形如 $f_n=af_{n-1}+bf_{n-W}$ 的形式，可以直接使用 Extremely Lagged Fibonacci 的做法来处理，不加优化的时间复杂度为 $\Theta((V/W)^2)$，这也足够了。

测试点 5,6,7,8（MP）

MP：Matrix Power，即矩阵快速幂。

这里所有点的权值都为 $1$，设邻接矩阵（带边权）为 $\bold M$，答案就可以表示为 $\bold M^{V-1}$ 的所有项之和。下面将根据 $\bold M$ 的不同性质来优化计算。

测试点 5：
没有什么特殊性质，用朴素的矩阵快速幂即可通过。

测试点 6：
可以观察到 $\bold M$ 是这个样子的：

$$\bold M=\begin{bmatrix} a_1 & a_2 & a_3 & \cdots & a_{n-1} & a_n \\ 1 & 0 & 0 & \cdots & 0 & 0 \\ 0 & 1 & 0 & \cdots & 0 & 0 \\0 & 0 & 1 & \cdots & 0 & 0 \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 0 & 0 & 0 & \cdots & 1 & 0 \end{bmatrix} $$

这是什么？经典的常系数线性递推的转移矩阵啊！设

$$F(x)=\frac{P(x)}{1-\sum_{i=1}^na_i x^i}$$

已知 $F(x) \bmod x^n=(1-x^n)/(1-x)$，由此可以计算出 $P(x)$（是一个小于 $n$ 次的多项式），而 $F(x)$ 的 $x^{V-1}$ 到 $x^{n+V-2}$ 项系数之和就是答案，即：

$$([x^{n+V-2}]-[x^{V-2}]) \frac{F(x)}{1-x}$$

还是用常系数线性递推的方法直接计算，时间复杂度 $\Theta(n \log n \log V)$。

测试点 7：
这里 $\bold M$ 是一个上三角矩阵，且主对角线上的值互不相同，由此可知其特征值就对应为主对角线上的值，而且 $\bold M$ 可以进行相似对角化。所以答案可以表示为

$$f_V=\sum_{i=1}^n c_i \lambda_i^V$$

的形式，这样就可以把 $V$ 对 $998244352$ 取模后再计算。设答案的生成函数为

$$F(x) = P(x) \prod_{i=1}^n \frac{1}{1-\lambda_i x}$$

由于 $\bold M$ 较为稀疏，其中 $F(x)$ 的前 $n$ 项是可以暴力计算的，然后就可以利用类似测试点 6 的方法求出 $P(x)$，然后就容易处理了。

测试点 8：

给定的图是这个样子的（其中所有奇数号点都有一个自环没有画出）：
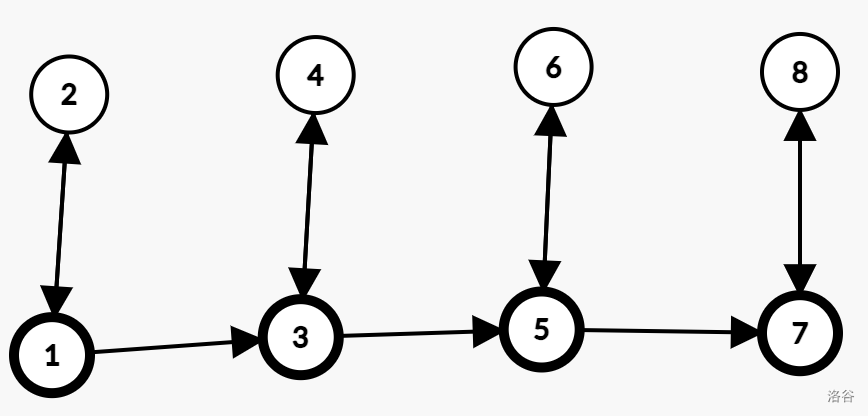
当然 $7$ 号点的后面还有，这里只是展示了一部分。

设 $F_k(x)$ 为从第 $k$ 大的奇数号点开始走的答案关于 $V$ 的生成函数，类似地设 $G_k(x)$ 表示偶数号点的情况，可以得到方程：

$$\begin{cases} F_k(x) = x(G_k(x)+F_k(x)+F_{k-1}(x)) +x \\ G_k(x) = xF_k(x)+ x\end{cases} $$

我们最终要求所有点的答案之和，可以直接求出

$$S_k(x)=F_k(x)+G_k(x)=\frac{xS_{k-1}(x)+2x}{1-x-x^2} $$

其中

$$S_1(x)=\frac{2x+x^2}{1-x-x^2}$$

这个递推式的形式简单，但是算起来有点复杂，设

$$P_k(x)=x^{k+1}+2x\frac{(1-x-x^2)^k-x^k}{1-2x-x^2}$$

可以解出

$$S_k(x)=\frac{P_k(x)}{(1-x-x^2)^k}$$

设 $N=n/2$，则答案为

$$[x^V]\sum_{k=1}^N S_k(x)=[x^V]\left( \frac{1+(n-4)x+(1-2n)x^2+(2-n)x^3}{(1-2x-x^2)^2}+\frac{x^{N+2}(1+x)^2}{(1-2x-x^2)^2(1-x-x^2)^N}\right) $$

简单分析一下，第一项中的分母，可以拆为 $(1-(1+\sqrt 2)x)^2(1-(1-\sqrt 2)x)^2$，这里 $\sqrt 2$ 在模 $998244353$ 意义下存在，所以这一项的值关于 $V$ 有长度为 $p(p-1)$ 的循环节。

对于第二项：

$$1-x-x^2=\left(1- \frac{1+\sqrt 5}{2}x\right)\left( 1-\frac{1-\sqrt 5}{2}x\right) $$

特征根在模意义下并不存在，但是其 $4p(p+1)$ 次方为 $1$。两部分综合一下，只需要将 $V$ 对 $4p(p+1)(p-1)$ 取模后计算即可。

测试点 9（R）

R：Ring，即环。

此数据点中的图是一个环，有 $n$ 条边的连通图。
考虑从一个点出发时，要先绕着环走 $\lfloor V/S \rfloor$ 圈（$S$ 为所有节点的权值和）。剩下的距离可以用一个区间 $[L,R]$ 来确定，每次 $L$ 增加 $1$，$R$ 依次往后扫找到合适的位置。

时间复杂度为 $\Theta(n + \log V)$，注意需要使用高精度除低精度来计算 $\lfloor V/S \rfloor$。

测试点 10（Finale）

每个点都有一个自环，除此之外没有其它的边，答案就非常简单了。顺带说一下这里的彩蛋：输入的节点权值其实是 ASCII 码，对应转换过来就是 Welcome to the end. Hope you enjoy my contest!。