自动搬运

查看原文

来自洛谷，原作者为

	jimmywang 基环内向树，二维前缀和，三碳化四铝，闪电五连鞭

搬运于2025-08-24 21:20:05，当前版本为作者最后更新于2020-07-31 15:46:47，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

口胡五分钟，代码两小时！

这个题啊，真是好写，也不好写。

好写呢，在于建个图，再跑一遍$Floyd$，比较最小值，就没了

不好写呢，就在于：

1.每个矩形只给了3个点.....

2.代码长（可能不是），相近的变量多（这是我）等等

来一步一步分析吧。。。

$0.$题意:

（略）

$1.$建图

$(1).$找到矩形的另外$1$个点

这个东西咋找呢？用亿点初中几何知识知道矩形是平行四边形，而平行四边形是对角线互相平分的。

如图所示：

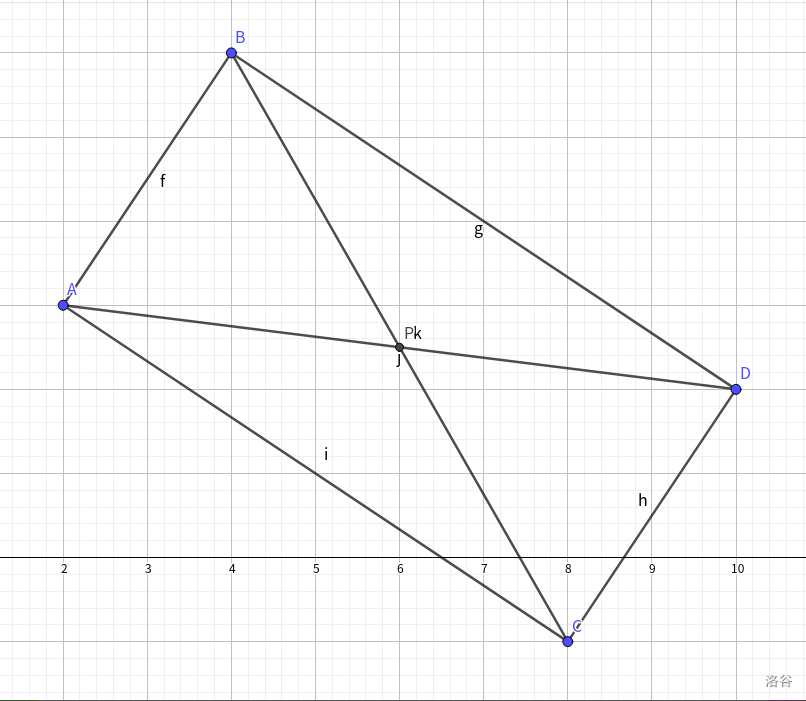
其中，点$A,B,C$为输入的点，$D$是所求的点，对角线交点为$P$

这个例子中，$BC$是一条对角线，$AD$是另一条。根据中点公式，可以得到

$$\begin{cases}x_P=\dfrac{x_B+x_C}{2}\\x_P=\dfrac{x_A+x_D}{2}\end{cases} $$$$\begin{cases}y_P=\dfrac{y_B+y_C}{2}\\y_P=\dfrac{y_A+y_D}{2}\end{cases} $$

所以可得

$$\begin{cases}x_D=x_B+x_C-x_A\\y_D=y_B+y_C-y_A\end{cases} $$

于是， 我们再用勾股定理判断一下哪两个点构成对角线，然后就能求出这个点啦！

$(2).$建图

这里我们发现题目给了两种路线，一种是城市之间的航空路线，一种是城市内部的公路。

所以建图的主要问题就在于判断两个点是否在同一城市内。

这个问题，要靠你标点的方式确定，此处就举本人的例子来说明。

我的想法是第$1$个城市标号$1,2,3,4$,第$2$个城市标号$5,6,7,8$,以此类推。

那么这些点的标号与对应的城市号有什么关系呢？

经过研究发现，若点的编号为$i$,则它对应的城市编号即为$(i-1)/4$（下取整）

于是这样就行了。

$2.$最短路

$emmm$，一看数据范围，$s \leq 100$

所以最多只有$400$个点，$O(n^3)$都能过。

那么$O(n^3)$的最短路是啥？$Floyd$啊~

跑一遍$Floyd$，然后求一下$A$的每个机场到$B$的每个机场的最小值就过了~

完整代码：

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define f(i,a,b) for(int i=a;i<=b;i++)
const ll inf=0x7f7f7f7f;
ll s,A,B,TTT;
double ans=inf,t,dis[410][410];
double x[410],y[410],T[110];
double diss(double x1,double y1,double x2,double y2){return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));}
double ds(double x1,double y1,double x2,double y2){return (x1-x2)*(x1-x2)+(y1-y2)*(y1-y2);}
int main() {
    scanf("%lld",&TTT);
    while(TTT--){
        memset(dis,0,sizeof(dis)),ans=inf;
        scanf("%lld%lf%lld%lld",&s,&t,&A,&B);
        f(i,1,s){
            scanf("%lf%lf%lf%lf%lf%lf%lf",&x[(i-1)*4+1],&y[(i-1)*4+1],&x[(i-1)*4+2],&y[(i-1)*4+2],&x[(i-1)*4+3],&y[(i-1)*4+3],&T[i]);
            double dab=ds(x[(i-1)*4+1],y[(i-1)*4+1],x[(i-1)*4+2],y[(i-1)*4+2]);
            double dac=ds(x[(i-1)*4+1],y[(i-1)*4+1],x[(i-1)*4+3],y[(i-1)*4+3]);
            double dbc=ds(x[(i-1)*4+2],y[(i-1)*4+2],x[(i-1)*4+3],y[(i-1)*4+3]);
            if(dab+dac==dbc)x[i*4]=x[(i-1)*4+2]+x[(i-1)*4+3]-x[(i-1)*4+1],y[i*4]=y[(i-1)*4+2]+y[(i-1)*4+3]-y[(i-1)*4+1];else
            if(dab+dbc==dac)x[i*4]=x[(i-1)*4+1]+x[(i-1)*4+3]-x[(i-1)*4+2],y[i*4]=y[(i-1)*4+1]+y[(i-1)*4+3]-y[(i-1)*4+2];else
            if(dbc+dac==dab)x[i*4]=x[(i-1)*4+2]+x[(i-1)*4+1]-x[(i-1)*4+3],y[i*4]=y[(i-1)*4+2]+y[(i-1)*4+1]-y[(i-1)*4+3];
        }
        f(i,1,s*4)f(j,1,s*4)if(i!=j){
                if((i-1)/4!=(j-1)/4)dis[i][j]=t*diss(x[i],y[i],x[j],y[j]);
                else dis[i][j]=T[(i-1)/4+1]*diss(x[i],y[i],x[j],y[j]);
            }
        f(k,1,s*4)f(i,1,s*4)f(j,1,s*4)dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);
        f(i,1,4)f(j,1,4)ans=min(ans,dis[(A-1)*4+i][(B-1)*4+j]);
        printf("%.1lf\n",ans);
    }
	return 0;
}