自动搬运

查看原文

来自洛谷，原作者为

	yummy 这个人是时代的眼泪，什么也没有留下

搬运于2025-08-24 22:56:08，当前版本为作者最后更新于2024-02-15 19:53:27，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

B. Swimming Pool 官方题解

本题涉及的主要知识点：

• 【1】几何（初中部分）
• 【2】if 语句
• （非必须）【3】绝对值函数

Part 1 判断是否构成四边形

要想构成梯形，首先要构成四边形。根据两点间线段最短可知，四条边可以构成四边形当且仅当任意一边小于另外三边之和，即 $p<q+r+s$ 等（共有 $4$ 个条件）。

其实把四个条件都写上已经可以完成这部分任务了，但是我们有没有更优雅的写法？

还是使用线段公理，我们可以把构成四边形（或其他多边形）的条件转化为”周长大于最长边长度的两倍“。从直观上看，如果你要用一个绳圈套住长 $l$ 的边，这个绳圈长度至少要 $2l$。

求最长边长度可以使用 max 求出：可以使用传统的 max(max(p,q),max(r,s))，也可以采用当前 NOI 系列比赛已经支持的 max({p,q,r,s}) 一次性求出四个数的最大值。

求和时注意数据类型，四个 $10^9$ 范围的数加起来可能会爆 int。

我怕本题 AC 率不够高，把 $10^9$ 改成 $5\times 10^8$ 了。

Part 2 判断四边形有没有可能是梯形

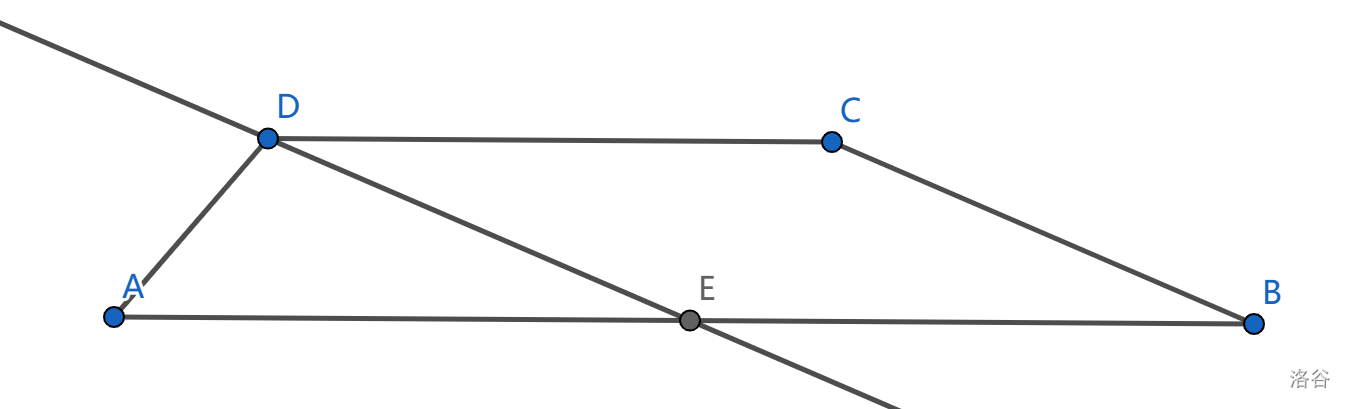
如图，假如有梯形 $ABCD$ 且 $AB//CD$，我们看看它需要满足的性质。

过 $D$ 作 $DE//BC$ 交 $AB$ 于 $E$。则 $AE$ 为 $p-r$，$AD$ 为 $s$，$DE$ 为 $q$。在三角形 $ADE$ 中，$|p-r|>|s-q|$。类似地，如果 $AD//BC$，那么 $|s-q|>|p-r|$。

这样我们就知道，如果要构成梯形，那么必须满足对边差不相等。反过来，对边差不相等的时候一定可以构成梯形吗？答案是肯定的，下面我们来证明这一点。

取对边差更大的一组对边（不妨认为是 $p,r$），以 $s,q,|p-r|$ 为边构造三角形 $ADE$。然后接下来延长 $AE$ 至 $B$ 使得 $AB=\max(p,r)$，再作平行四边形 $DEBC$ 即可。

Part 3 参考代码

C++ 代码：

#include<bits/stdc++.h>
using namespace std;
int T;
long long p,q,r,s;
int main(){
	for(scanf("%d",&T);T;T--){
		scanf("%lld%lld%lld%lld",&p,&q,&r,&s);
		if(2*max({p,q,r,s}) >= p+q+r+s or abs(p-r)==abs(q-s))
			puts("no");
		else puts("yes");
	}
	return 0;
}

Python 3 代码：

for i in range(int(input())):
    p,q,r,s=map(int,input().split())
    if 2*max(p,q,r,s)>=p+q+r+s or abs(p-r)==abs(q-s):
        print("no")
    else:
        print("yes")