自动搬运

查看原文

来自洛谷，原作者为

	scp020 这是一个亖人 || 最后在线时间：2025年8月24日9时5分

搬运于2025-08-24 22:56:03，当前版本为作者最后更新于2024-03-09 21:30:04，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

P10237 [yLCPC2024] E. Latent Kindom 题解

简单的单 $\log$ 做法，不用会任何的数据结构就可以看懂。

解法

考虑把每个序列 $a_i$ 升序排序，这样方便我们二分。

考虑将两个序列 $a_x,a_y$ 合并，即选出在这两个序列中排名为 $\lceil \dfrac{len_x+len_y}{2} \rceil$ 的数，我们把合并后的序列分为两部分，一部分是小于等于中位数的，一部分是大于中位数的。我们发现小于等于中位数的那部分在 $a_x$ 和 $a_y$ 里是连续分布的，故我们考虑二分小于等于中位数的那部分在 $a_x$ 中的分布情况。如图，该部分分布情况即为两个竖线左侧的连续区间。

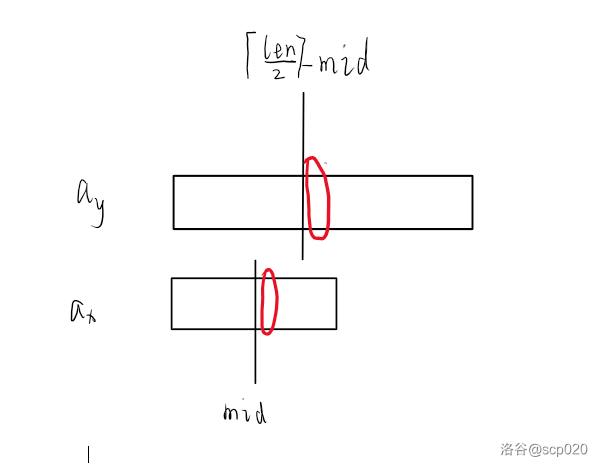
当前 $mid$ 合法当且仅当 $a_{x,mid}$ 和 $a_{y,\lceil \frac{len}{2} \rceil -mid}$ 都小于等于红色圈起来的两个数（即黑色竖线右侧的两个数）。

考虑如何移动二分的 $l,r$。当上面的黑色竖线比下面的红色圈大时，我们要把上面的黑色竖线向左移动，下面的黑色竖线向右移动；否则我们就把下面的黑色竖线向左移动，上面的黑色竖线向右移动，直到当前 $mid$ 合法。

复杂度分析：排序复杂度 $\mathcal{O}(n \log l)$，查询复杂度 $\mathcal{O}(q \log l)$，所以总复杂度 $\mathcal{O}((n+q) \log l)$。

在排序时这里有个小 trick，就是在 $a_i$ 的前后放置两个标兵，一个极小值，一个极大值，防二分时越界。

代码

#include<bits/stdc++.h>
namespace fast_IO
{
	/**
	 * 快读快写
	*/
};
using namespace fast_IO;
#define int long long
int t,n,q,len[1000010];
std::vector<int> v[1000010];
inline int check(int x,int y,int lx,int ly)
{
	int midi=std::max(v[x][lx],v[y][ly]);
	if(midi<=v[x][lx+1] && midi<=v[y][ly+1]) return 1;
	if(midi>v[x][lx+1]) return 0;
	return 2;
}
signed main()
{
	in>>t;
	while(t--)
	{
		in>>n>>q;
		for(int i=1,x;i<=n;i++)
		{
			in>>len[i],v[i].clear(),v[i].push_back(-1),v[i].push_back(0x7fffffffffffffff);
			for(int j=1;j<=len[i];j++) in>>x,v[i].push_back(x);
			std::sort(v[i].begin(),v[i].end());
		}
		for(int i=1,tlen,x,y,l,r,mid,ret,ans;i<=q;i++)
		{
			in>>x>>y,tlen=len[x]+len[y],tlen=ceil(tlen/2.0);
			l=std::max(0ll,tlen-len[y]),r=std::min(len[x],tlen);
			while(l<=r)
			{
				mid=(l+r)/2,ret=check(x,y,mid,tlen-mid);
				if(ret==1)
				{
					ans=std::max(v[x][mid],v[y][tlen-mid]);
					break;
				}else if(ret==0) l=mid+1;
				else r=mid-1;
			}
			out<<ans<<'\n';
		}
	}
	fwrite(Ouf,1,p3-Ouf,stdout),fflush(stdout);
	return 0;
}