自动搬运

查看原文

来自洛谷，原作者为

	小明小红 寄ด้้้้้็้้้็็็็็้้้้้็็็็็้้้้้้็็็็็้้้้้็็็็็้้้้้้็็็็็้้้้้็็็็็้้้้้้็็็็็้้้้้็็็็็้้้้้้็็

搬运于2025-08-24 22:56:02，当前版本为作者最后更新于2024-07-17 11:33:17，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

P10236题解

前言：

黑润心有错夏令营讲了这道题，我本想抄题解的，结果发现看不懂前几篇，只能自己写一篇啦。

正文：

算法判断：

我们可以发现这个操作只能删去头和尾，所以无论经过多少次合法的操作，得到的数组一定是原串的子串。什么？连续？好！区间动态规划，启动！

状态定义：

我们定义 $dp_{l,r,0}$ 为 $[l,r]$ 序列下一个将删去最左边的数的最大得分，同理 $dp_{l,r,1}$ 为 $[l,r]$ 序列下一个将删去最右边的数的最大得分。

如何转移：

我们知道 $[l,r,0/1]$ 一定是由 $[l-1,r,0]$ 或 $[l,r+1,1]$ 转移而来，转移是有得分的，如何计算得分？

计算得分：

举个栗子：

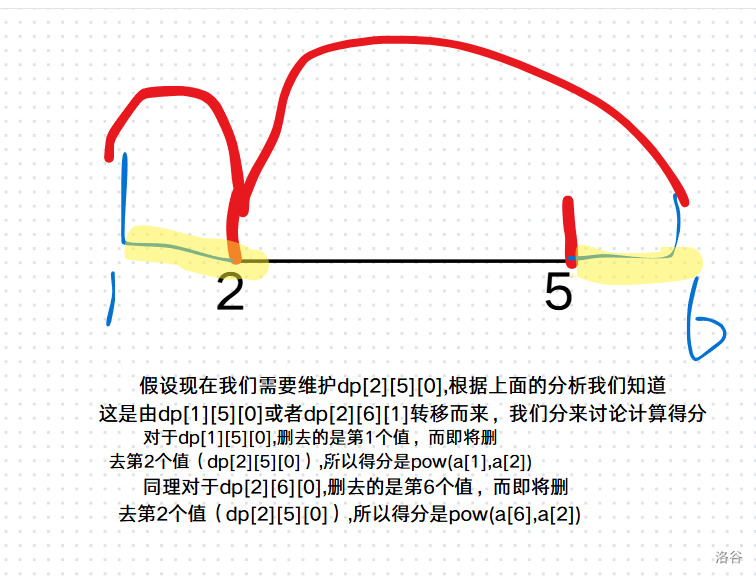
推出方程

我们现在就可以推出方程了：

$dp_{i,j,0}=\max(dp_{i-1,j,0}+a_{i-1}^{a_i},dp_{i,j+1,1}+a_{j+1}^{a_i})$

$dp_{i,j,1}=\max(dp_{i-1,j,0}+a_{i-1}^{a_j},dp_{i,j+1,1}+a_{j+1}^{a_j})$

得到答案

根据题意我们的答案是 $\max(dp_{i,i,0},dp_{i,i,1})$ 其中 $i$ 为 $1$ 到 $n$ 的任意整数。

补充

我们现在把代码交了上去交了，啊？为什么不对？

对了！记得要用快速幂，还一定要特判 $0^0=0$。

code

#include<bits/stdc++.h>
using namespace std;
#define ll long long
ll mod=998244353;
ll quickpow(ll x,ll y)
{
	if(x==0&&y==0)
	{
		return 0;//特判！！！ 
	}
	ll ans=1,p=x;
	while(y>0)
	{
		if(y&1)
		{
			ans=(ans*p)%mod;
		}
		p=(p*p)%mod;
		y>>=1;
	}
	return ans;
}
ll T,dp[1009][1009][2],a[1009],n; 
int main()
{
	cin>>T;
	while(T--)
	{
		cin>>n;
		for(ll i=1;i<=n;i++)
		{
			cin>>a[i];
		}
		memset(dp,0,sizeof(0));//多测清空 
		for(ll len=n;len>=1;len--)//按题目顺序枚举长度 
		{
			for(ll i=1;i<=n-len+1;i++)//枚举左右端点 
			{
				ll j=i+len-1;
				dp[i][j][0]=max(dp[i-1][j][0]+quickpow(a[i-1],a[i]),dp[i][j+1][1]+quickpow(a[j+1],a[i]));
				dp[i][j][1]=max(dp[i-1][j][0]+quickpow(a[i-1],a[j]),dp[i][j+1][1]+quickpow(a[j+1],a[j]));
			}
		}
		ll ans=0;
		for(ll i=1;i<=n;i++)//统计答案 
		{
			ans=max(ans,dp[i][i][0]);
			ans=max(ans,dp[i][i][1]);
		}
		cout<<ans<<endl;
	}
	return 0;
 }