自动搬运

查看原文

来自洛谷，原作者为

	云浅知处 喵

搬运于2025-08-24 22:55:28，当前版本为作者最后更新于2024-02-19 20:06:08，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

考虑对每个限制 $(u_i,v_i)$ 连无向边 $(u_i,v_i)$。

• 若图中有至少两个连通块，任选两个连通块，在这两个连通块中各任取一点 $x,y$，考虑如下构造：称 $x$ 所在连通块中的所有点为黑点，剩余点为白点，将所有黑点向 $y$ 连边，所有白点向 $x$ 连边。这样，任意两个同一连通块中的点的距离均为 $2$。以下是一个图示：

• 

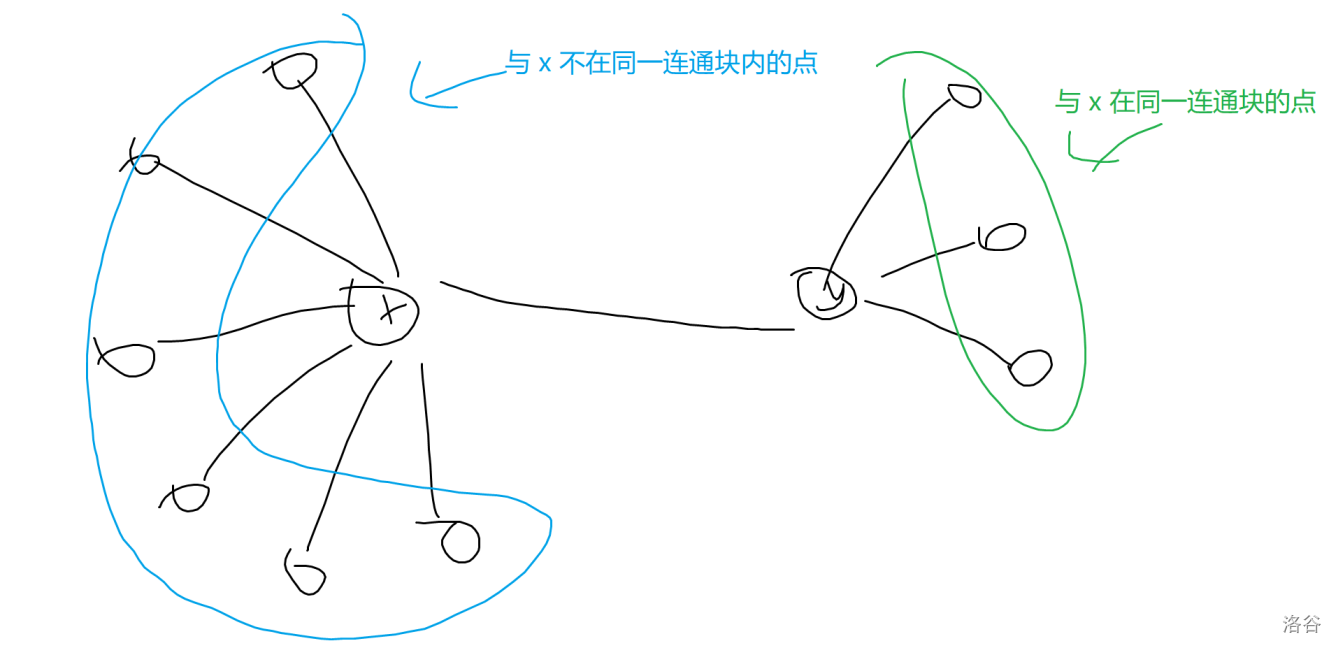
• 若图中有且仅有一个连通块，我们证明此时无解：考虑将原树黑白染色，在所有同色点之间连边，则给出的图必定是该图的生成子图。由于原图有且仅有两个连通块，因此给出的图必然至少存在两个连通块；从而此时不存在这样的树。

算法的时间复杂度为 $O(n+m)$。

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;

int T, n, m, fa[N];

inline int getfa(int x) {return x == fa[x] ? x : fa[x] = getfa(fa[x]);}

int main() {
	scanf("%d", &T);
	while (T--) {
		scanf("%d%d", &n, &m);
		for (int i = 1; i <= n; ++i) fa[i] = i;
		for (int i = 1, x, y; i <= m; ++i) {
			scanf("%d%d", &x, &y);
			assert(x != y);
			x = getfa(x); y = getfa(y);
			fa[x] = y;
		}
		int cnt = 0; int p[2];
		for (int i = 1; i <= n; ++i) {
			if (getfa(i) != i) continue;
			if (cnt < 2) p[cnt] = i;
			cnt++;
		}
		if (cnt == 1 && n > 1) {
			puts("No");
			continue;
		}
		if (cnt == 1 && n == 1) {
			puts("Yes");
			continue;
		}
		puts("Yes");
		printf("%d %d\n", p[0], p[1]);
		for (int i = 1; i <= n; ++i) {
			if (i == p[0] || i == p[1]) continue;
			if (getfa(i) == p[0]) printf("%d %d\n", i, p[1]);
			else printf("%d %d\n", i, p[0]);
		}
	}
	return 0;
}