1 条题解

  • 0
    @ 2025-8-24 22:55:23

    自动搬运

    查看原文

    来自洛谷，原作者为

    avatar gghack_Nythix
    ‎

    搬运于2025-08-24 22:55:23，当前版本为作者最后更新于2024-02-18 20:39:16，作者可能在搬运后再次修改，您可在原文处查看最新版

    自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

    以下是正文

    前言：这篇题解是纯暴力，但是居然跑到了最优解前5。

    分析:

    加强前:

    没什么好分析的，你很容易就可以写出下面的代码:

    #include<bits/stdc++.h>
using namespace std;
int a[50005],n,l,r,maxx,ans;
int tot[400005];
inline bool ck(int k,int ragez){
	for(int i = 1;i <= n;++i) { 
		if(tot[a[i] % k] == ragez) return 0;
		tot[a[i] % k] = ragez;
	} 	
	return 1;
}
signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	cin >> n >> l >> r;
	for(register int i = 1;i <= n;++i) { 
		cin >> a[i]; 
		maxx = max(a[i],maxx); 
		if(tot[a[i]] == 1){
			cout << 0 ;
			return 0;
		}
		tot[a[i]] = 1;
	} 	
	memset(tot,0,sizeof(tot));
	l = max(n,l);
	if(r > maxx) ans += r - maxx + 1;//计算绝对有解的
	int curr = 0;
	for(register int k = l;k <= min(r,maxx - 1);++k) { ++ curr;if(ck(k,curr)) {++ans;} } 
	cout << ans ;
	return 0;
}

    在不加强时可以AC，加强后可以通过21个点。

    优化:

    可以寻找到一部分比当前模数小的数，对这一部分进行标记，表示这些取模后仍然是他本身。容易发现，即使 kk 继续扩大，这一部分依然不用被计算。所以每次直接跳过就可以了

    #include<bits/stdc++.h>
#define max(x,y) (x>y?x:y)
using namespace std;
int a[50005],n,l,r,maxx,ans,lst,tmp,curr,tot[400005],sqrtsqrt;
bool tot2[400005],toto[400005];
inline bool ck(int k,int ragez){
	while(a[lst] < k && lst <= n) ++ lst,tot2[a[lst]] = 1;//这些一定不需要
	for(int i = lst;i <= n;++i) { 
		tmp = a[i] % k;
		if(tot[tmp] == ragez || tot2[tmp]) return 0;
		tot[tmp] = ragez;
	} 	
	return 1;
}
signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	cin >> n >> l >> r;
	for(int i = 1;i <= n;++i) { 
		cin >> a[i];
		maxx = max(a[i],maxx); 
		if(toto[a[i]] == 1){
			cout << 0;
			return 0;
		}
		toto[a[i]] = 1;
	} 
	sort(a + 1,a + n + 1);
	memset(tot,0,sizeof(tot));
	l = max(n,l);
	if(r > maxx) ans += r - maxx + 1;
	sqrtsqrt = sqrt(n);
	for(int k = l;k <= min(r,maxx - 1);++k) { 
		if(ck(k,++curr)) ++ans;
	} 
	cout << ans ;
	return 0;
}

    第二次优化:

    发现我们可以使用一些原数列本来剩下的值，用这些值去制造一个和他同余的数，如果这个同余的数已经在原序列存在了，那么也就说明冲突了。

    如何制造呢?

    设 n=fk+yn=fk+y，其中 kk 就是题面要求的 kk 。yy 为对 kk 取余的余数。

    则 n′=(f+f′)k+y=fk+f′k+yn' = (f+f')k+y = fk + f'k + y 。

    也就是说枚举 kk 的多少倍就可以了。

    #include<bits/stdc++.h>
#define max(x,y) (x>y?x:y)
#define I_love_You() (assert(n <= 11451441))
using namespace std;
int a[50005],n,l,r,maxx,ans,lst,tmp,curr,tot[400005],sqrtsqrt;
bool tot2[400005],toto[400005];
inline bool ck(int k,int ragez){
	while(a[lst] < k && lst <= n) ++ lst,tot2[a[lst]] = 1;//这些一定不需要
	for(int i = lst;i <= n;++i) { 
		tmp = a[i] % k;
		if(tot[tmp] == ragez || tot2[tmp]) return 0;
		tot[tmp] = ragez;
	} 	
	return 1;
}
signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	cin >> n >> l >> r;
	for(int i = 1;i <= n;++i) { 
		cin >> a[i];
		maxx = max(a[i],maxx); 
		if(toto[a[i]] == 1){
			cout << 0;
			return 0;
		}
		toto[a[i]] = 1;
	} 
	sort(a + 1,a + n + 1);
	memset(tot,0,sizeof(tot));
	l = max(n,l);
	if(r > maxx) ans += r - maxx + 1;
	sqrtsqrt = sqrt(n);
	for(int k = l;k <= min(r,maxx - 1);++k) { 
		if(k >= sqrtsqrt) {
			for(int i = 1;i <= sqrtsqrt;++i) {
				for(int j = a[i] + k;j <= a[n];j += k) {
					if(toto[j]) goto nimade;
				}
			}
		}
		if(ck(k,++curr)) ++ans;
		nimade: I_love_You();
	} 
	cout << ans ;
	return 0;
}

    好嘛，差几个点AC。

    又叕叕优化:

    容易发现，如果 k>ax−ayk > a_x - a_y ，可以说明在 [x,y][x,y] 区间中的数对kk取模一定是不会冲突的，最坏情况下会剩下 k−ax+ayk - a_x + a_y 个余数没有被使用。

    对于 aya_y 的选择，自然是选择小于 aya_y 时，这个数不冲突，消除干扰。

    #include<bits/stdc++.h>
#define max(x,y) (x>y?x:y)
#define I_love_You() (assert(n <= 11451441))
using namespace std;
int a[50005],n,l,r,maxx,ans,lst,tmp,curr,tot[400005],sqrtsqrt,f[400005];
bool tot2[400005],toto[400005];
inline bool ck(int k,int ragez){
	while(a[lst] < k && lst <= n) ++ lst,tot2[a[lst]] = 1;//这些一定不需要
	for(int i = lst;i <= n;++i) { 
		tmp = a[i] % k;
		if(tot[tmp] == ragez || tot2[tmp]) return 0;
		tot[tmp] = ragez;
	} 	
	return 1;
}
inline bool cky(int k,int ragez){
	while(a[lst] < k && lst <= sqrtsqrt) ++ lst,tot2[a[lst]] = 1;//这些一定不需要
	for(int i = lst;i <= sqrtsqrt;++i) { 
		tmp = a[i] % k;
		if(tot[tmp] == ragez || tot2[tmp]) return 0;
		tot[tmp] = ragez;
	} 	
	return 1;
}
signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	cin >> n >> l >> r;
	for(int i = 1;i <= n;++i) { 
		cin >> a[i];
		maxx = max(a[i],maxx); 
		if(toto[a[i]] == 1){
			cout << 0;
			return 0;
		}
		toto[a[i]] = 1;
	} 
	sort(a + 1,a + n + 1);
	memset(tot,0,sizeof(tot));
	l = max(n,l);
	if(r > maxx) ans += r - maxx + 1;
	sqrtsqrt = 0.4376 * sqrt(n);
	for(int k = l;k <= min(r,maxx - 1);++k){ 
		while(!cky(k,++curr)) --sqrtsqrt;
		if(cky(k,++curr)) break;
	}
	for(int k = l;k <= min(r,maxx - 1);++k) { 
		if(k >= sqrtsqrt) {
			for(int i = 1;i <= sqrtsqrt;++i) {
				for(int j = a[i] + k;j <= a[n];j += k) {
					if(toto[j]) goto nimade;//存在同余
				}
			}
		}
		if(k > a[n] - a[sqrtsqrt]) {++ans;continue;}
		if(ck(k,++curr)) ++ans;
		nimade: I_love_You();
	} 
	cout << ans ;
	return 0;
}

    T掉了最后一个点。

    继续优化:

    发现这个程序在序列中数字比较连续时容易TLE。那么我们对于这种连续（即ai+1=ai+1a_i+1=a_{i+1}）的块一个个做处理。

    做处理时，我们不妨换一种思路，不对原数进行显著的放入桶判断模数相等，而是转化成线段覆盖问题:

    设当前两个块分别是AA，BB，块中的起始，终止元素对 kk 取余的结果为stst，eded:

    考虑记录这两个块中的起始元素和终止元素，这之中的余数一定不会离散的分布，但注意，他们之间的模数有几率变回0。

    1. 先考虑两个块不变回0的情况，即ABAB的eded均大于stst:

    此时的线段长这个样子:

    T1

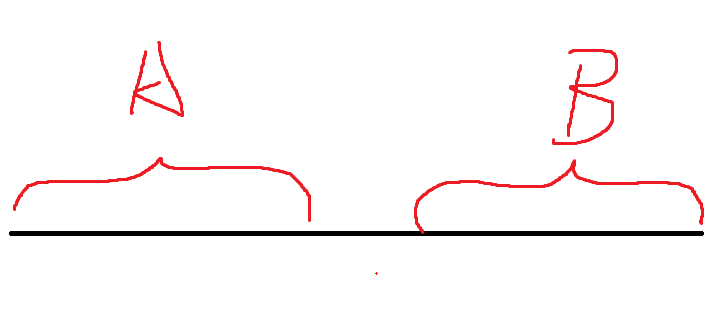
    只需要判断两条线段是否相交。

    1. 其中一个分裂成两条线段:

    此时长这个样子:

    T2

    可以判断另外一套线段是否和空白区相交。

    1. 两个都分裂了:

    此时长这个样子

    T3

    我是将其中一个线段分成 [st,k−1][st,k-1] 和 [0,ed][0,ed] 来判断的，当然仔细想想这种情况明显不成立。

    讨论完之后就可以愉快的写代码了，时间复杂度应该也是 O(n2)O(n^2) 左右的:

    #include<bits/stdc++.h>
#define max(x,y) (x>y?x:y)
#define I_love_You() (assert(n <= 11451441))
using namespace std;
int a[50005],n,l,r,maxx,ans,lst,tmp,curr,tot[400005],sqrtsqrt,f[400005],cntt;
bool tot2[400005],toto[400005];
struct node{
	int len,st,ed;
	bool operator < (const node & hh) const {
		return len > hh.len;
	}
};
vector<node> vec;
inline bool ck(int k,int ragez){
	while(a[lst] < k && lst <= n) ++ lst,tot2[a[lst]] = 1;//这些一定不需要
	for(int i = lst;i <= n;++i) { 
		tmp = a[i] % k;
		if(tot[tmp] == ragez || tot2[tmp]) return 0;
		tot[tmp] = ragez;
	} 	
	return 1;
}
inline bool cky(int k,int ragez){
	while(a[lst] < k && lst <= sqrtsqrt) ++ lst,tot2[a[lst]] = 1;//这些一定不需要
	for(int i = lst;i <= sqrtsqrt;++i) { 
		tmp = a[i] % k;
		if(tot[tmp] == ragez || tot2[tmp]) return 0;
		tot[tmp] = ragez;
	} 	
	return 1;
}
inline int qp(int a,int b){
	int ans = 1;
	while(b) {
		if(b & 1) ans = ans * a;
		a = a * a;
		b >>= 1;
	}
	return ans;
}
namespace gghack{
	inline bool cka(int k){
		for(int i = 0;i < signed(vec.size());++i) {//前面的和当前的比较
			for(int j = 0;j < i;++j) {//枚举前面的
				if(vec[i].st % k <= vec[i].ed % k){
					int lftmd = 0,rgtmd = 0,mode = 0;
					if(vec[j].st % k > vec[j].ed % k || (vec[j].ed % k - vec[j].st % k + 1) != vec[j].len) {//取模爆掉了成为了0
						lftmd = vec[j].ed,rgtmd = vec[j].st;//有剩余格子的就是这一坨
						mode = 1;//成为判断是否不在冲突范围中
					}
					else lftmd = vec[j].st,rgtmd = vec[j].ed;
					if(mode) {//相当于两条断开的线段和一条完整的线段判断线段覆盖
						if(!(vec[i].st % k > lftmd && vec[i].ed % k < rgtmd))return 0;//不在空闲的那一坨
					}
					else {
						if((vec[i].st % k >= lftmd && vec[i].ed % k <= rgtmd) || (vec[i].st % k >= lftmd && vec[i].st % k <= rgtmd) || (vec[i].ed % k <= rgtmd && vec[i].ed % k >= lftmd) || (vec[i].st % k <= lftmd && vec[i].ed % k >= rgtmd))return 0;//不在外面的那一坨白色区域
					}
				}
				else {//这一波也是拆成两个线段，一个是st ~ k - 1，一个是0 ~ ed
					int lftmd = 0,rgtmd = 0,mode = 0;
					if(vec[j].st % k > vec[j].ed % k || (vec[j].ed % k - vec[j].st % k + 1) != vec[j].len) {//取模爆掉了成为了0
						lftmd = vec[j].ed,rgtmd = vec[j].st;//有剩余格子的就是这一坨
						mode = 1;//成为判断是否不在冲突范围中
					}
					else lftmd = vec[j].st,rgtmd = vec[j].ed;
					if(mode) {//相当于两条断开的线段和一条完整的线段判断线段覆盖
						if(!(vec[i].st % k > lftmd && k < rgtmd))return 0;//不在空闲的那一坨
						if(!(0 > lftmd && vec[i].ed % k < rgtmd))return 0;//不在空闲的那一坨
					}
					else {
						if((vec[i].st % k >= lftmd && k <= rgtmd) || (vec[i].st % k >= lftmd && vec[i].st % k <= rgtmd) || (k - 1 <= rgtmd && k - 1 >= lftmd) || (vec[i].st % k <= lftmd && k - 1 >= rgtmd))return 0;//不在外面的那一坨白色区域
						if((0 >= lftmd && vec[i].ed % k <= rgtmd) || (0 >= lftmd && 0 <= rgtmd) || (vec[i].ed % k <= rgtmd && vec[i].ed % k >= lftmd) || (0 <= lftmd && vec[i].ed % k >= rgtmd))return 0;//不在外面的那一坨白色区域
					}
				}
			}
		}
		return 1;
	}
	void tohack(){
		for(int k = l;k <= min(maxx - 1,r);++k) {if(cka(k))++ans;}
		cout << ans << '\n';
		exit(0);
	}
}
signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	cin >> n >> l >> r;
	for(int i = 1;i <= n;++i) { 
		cin >> a[i];
		maxx = max(a[i],maxx); 
		if(toto[a[i]] == 1){
			cout << 0;
			return 0;
		}
		toto[a[i]] = 1;
	} 
	sort(a + 1,a + n + 1);
	memset(tot,0,sizeof(tot));
	l = max(n,l);
	if(r > maxx) ans += r - maxx + 1;
	sqrtsqrt = sqrt(n);//玄学调参
	for(int k = l;k <= min(r,maxx - 1);++k){ 
		while(!cky(k,++curr)) --sqrtsqrt;//余数冲突满足单调性
		if(cky(k,++curr)) break;//这个都符合了，下一个更大的余数会被映射到更大的空间，可以跳过
	}
	int d = 1;
	for(int i = 2;i <= n + 1;++i) {
		if(a[i - 1] + 1 != a[i]){
			vec.emplace_back(node{d,a[i - d],a[i - 1]});
			d = 1;
			++i;
		}
		++d;
	}
	if(vec.size() >= 2 && vec.size() <= sqrt(sqrt(n))){gghack::tohack();return 0;}
	for(int k = l;k <= min(r,maxx - 1);++k) { 
		if(k >= sqrtsqrt) {
			for(int i = 1;i <= sqrtsqrt;++i) {
				for(int j = a[i] + k;j <= a[n];j += k) {
					if(toto[j]) goto nimade;//存在同余
				}
			}
		}
		if(k > a[n] - a[sqrtsqrt]) {++ans;continue;}
		if(ck(k,++curr)) ++ans;
		nimade: I_love_You();
	} 
	cout << ans << '\n';
	return 0;
}

    后记:

    doge

    卡不掉应该也差不多了吧，毕竟只要解决题目都可以。

    • 1

    [DTCPC 2024] 取模

    信息

    ID
    9806
    时间
    1000ms
    内存
    512MiB
    难度
    5
    标签
    递交数
    0
    已通过
    0
    上传者
    1. 关于
    2. 联系我们
    3. 隐私
    4. 服务条款
    5. Language
    6. 主题
    3. Worker 0, 26ms