自动搬运

查看原文

来自洛谷，原作者为

	CleverRaccoon 不蓝钩不改个签

搬运于2025-08-24 22:54:47，当前版本为作者最后更新于2024-02-09 18:52:28，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

首先祝大家除夕快乐！新年快乐！

题目

一句话题意：求将 $M$ 种奖品共 $N\sim N+1$ 个发给 $N$ 个人有多少种方案。

思路

很明显，此题考察组合数学。

把每个人想象成一个位置，然后将奖品一类一类地依次填充到这些位置中。需要应用到组合数 $C_{n}^{m}$，根据组合数公式 $C_{n}^{m}=C_{n-1}^{m}+C_{n-1}^{m-1}$ 可以预处理出来。那么为什么不是排列而是组合呢？因为一位同学获得了不同种类的奖品，才算是不同的方案。而如果求排列，假设第 $k$ 类奖品有 $p$ 个，那么这位同学拿到第 $k$ 奖品的第 $1$ 个和拿到第 $p$ 个就会被视为不同的方案，显然不符合题意。

通过例子来解释，比如样例一的第一组数据：

3 2 1 2

三个人，两种奖品，每种奖品分别有 $1$ 个和 $2$ 个。

• 首先考虑第一种物品。第一种物品有 $1$ 个，它有 $3$ 个位置可以选择，故有 $C_{3}^{1}=3$ 种方案。

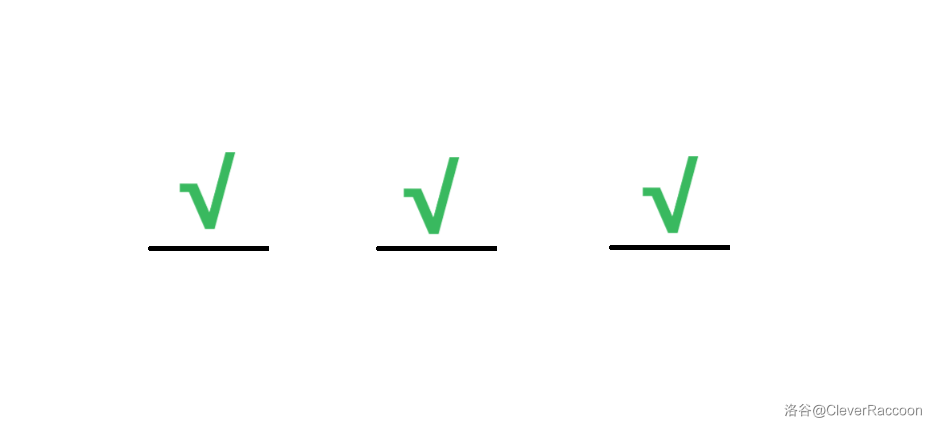
• 接着，考虑第二种物品。第二种物品有 $2$ 个，无论第一种物品选择了哪个位置，都只剩下 $3-1=2$ 个位置供它选择了，故有 $C_{2}^{2}=1$ 种方案。

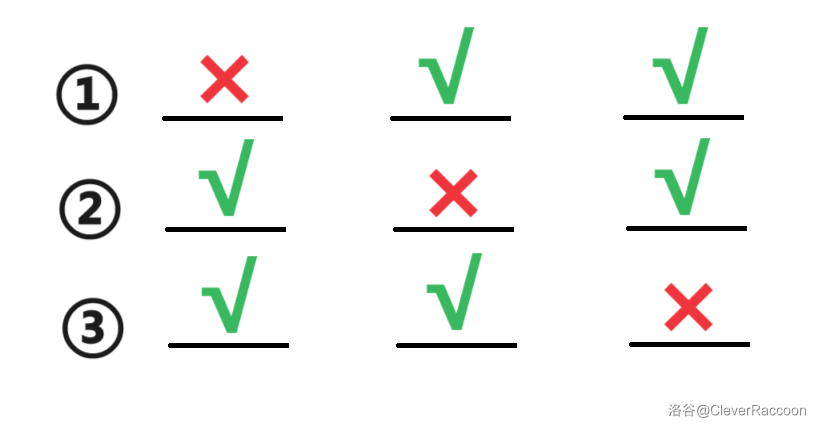
根据乘法原理，因为几次选择是顺次进行的，所以将两次选择的方案数乘起来即为答案。

于是，我们便得到了一份代码。但别着急，因为这份代码存在问题。

#include <bits/stdc++.h>
using namespace std;
const int MOD=1e9+7;
const int N=1005;
int T,n,m,ls,a[N],c[N][N],ans;
void init(){	// 初始化组合
	for(int i=0;i<N;i++)
		for(int j=0;j<=i;j++)
			if(j==0)c[i][j]=1;
			else c[i][j]=(c[i-1][j]+c[i-1][j-1])%MOD;	// 记得取模
}
int main(){
	init();
	cin>>T;
	while(T--){
		cin>>n>>m;
		for(int i=1;i<=m;i++)cin>>a[i];
		ans=1;
		for(int j=1,ls=n;j<=m;j++){	// 每一种奖品
			ans=(1ll*ans*c[ls][a[j]])%MOD;	// 注意转化为 long long 类型后再取模，否则有可能爆 int
			ls-=a[j];	// 将还未领奖品的人数，即空的位置数减一
		}
		cout<<ans%MOD<<"\n";
	}
	return 0;
}

棘手的问题

我们会发现，由于 $a_0+a_1+\cdots+a_{M-1}$ 有可能等于 $N+1$，而上述的做法只能解决等于 $N$ 的情况。

那么怎么做呢？我们发现，多出来的那一个奖品其实就相当于发给了空气，那么就把空气也当成是一个人，它也参与领取奖品就好了。

我们在上面代码的基础上进行了修改，计算出 $a_0+a_1+\cdots+a_{M-1}$ 的值，然后他如果超过了 $N$，就将初始总人数加一。

#include <bits/stdc++.h>
using namespace std;
const int MOD=1e9+7;
const int N=1005;
int T,n,m,ls,a[N],c[N][N],ans,sum;
void init(){	// 初始化组合
	for(int i=0;i<N;i++)
		for(int j=0;j<=i;j++)
			if(j==0)c[i][j]=1;
			else c[i][j]=(c[i-1][j]+c[i-1][j-1])%MOD;	// 记得取模
}
int main(){
	init();
	cin>>T;
	while(T--){
		cin>>n>>m;
		sum=0;	// sum 记录奖品总数
		for(int i=1;i<=m;i++)cin>>a[i],sum+=a[i];	// 输入的同时更新 sum
		ans=1;
		// ls=n+(sum>n) 表示如果 sum>n，那么 ls=n+1，否则 ls=n，即解决上面所说的问题
		for(int j=1,ls=n+(sum>n);j<=m;j++){	// 每一种奖品
			ans=(1ll*ans*c[ls][a[j]])%MOD;	// 注意转化为 long long 类型后再取模，否则有可能爆 int
			ls-=a[j];	// 将还未领奖品的人数，即空的位置数减一
		}
		cout<<ans%MOD<<"\n";
	}
	return 0;
}

这样，我们就可以通过本题了。