自动搬运

查看原文

来自洛谷，原作者为

	CYZZ 能卷是一种幸运

搬运于2025-08-24 22:54:28，当前版本为作者最后更新于2024-01-20 19:57:34，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

P10080

考场上想到做法，结果忘了匈牙利和网络流，后悔莫及。但现在看来就算会了也写不出来，膜拜 @缪凌锴_Mathew 大师场切。

前置知识

二分图最大匹配，找环。

思路

题目要求找一个黑色边数量为偶数的匹配，这是一个很好的切入口，可以排除掉很多奇怪的算法。

假设现在你已经找到了一个完美匹配（找不到直接无解），称匹配中的边为原配边，此时黑色边的数量无非就两种情况：

1. 黑色边的数量为偶数，此时直接输出匹配即可。
2. 黑色边的数量为奇数，此时我们考虑对匹配进行调整，使黑边数量的奇偶性改变。

稍加思考可以发现，只需要找到一个环，满足环上黑边数量为奇数，且原配边占环的一半（即隔一条有一条原配边）。调整时，把环上的原配边调整为环上的非原配边即可。

如何找到这个环呢？发现在求解完美匹配后的残量网络里，恰好改变了原配边的方向。也就是说，我们只需要在残量网络中找奇环即可。

可能讲得有一点抽象，配个样例的图理解一下：

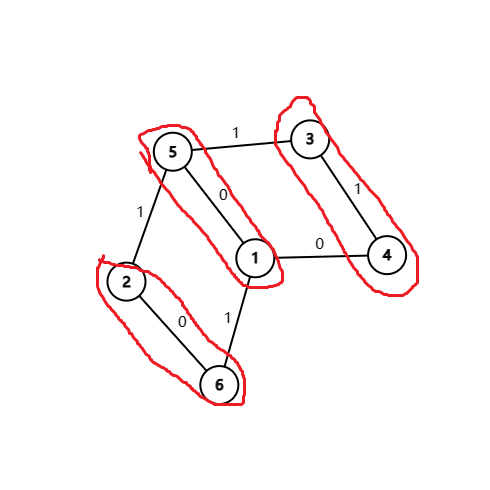
以上是残量网络：如果我们已经找到了完美匹配 $(3,4),(1,5),(2,6)$，然后发现边权和为奇数。接着我们找到了一个奇环 $5\rightarrow1\rightarrow6\rightarrow2\rightarrow5$，就用 $(1,6),(2,5)$ 替换掉 $(5,1),(6,2)$，最后得到正确匹配 $(3,4),(1,6),(2,5)$。

需要注意的是：找环不能单纯地以每个点为根节点都 bfs 一次，这样是 $\mathcal{O(nm)}$ 的。应该使用 dfs，同时不要重复点,这是 $\mathcal{O(n+m)}$ 的。拆点的意思是由 $(u,val)$ 走到 $(v,val\oplus w)$，$val,w$ 分别表示当前的奇偶性和当前边的权值。

如果使用 dinic 求解完美匹配的话，瓶颈在网络流，时间复杂的 $\mathcal{O(m\sqrt{n})}$。

代码

#include <bits/stdc++.h>
using namespace std;
#define N 1005
#define M 600005
int n,m,S,T;
int tot=1,head[N];
struct Edge
{
    int next,to,w,val;
}e[M];
void add_edge(int u,int v,int w1,int w2)
{
    e[++tot].next=head[u];
    e[tot].to=v;
    e[tot].w=w1;
    e[tot].val=w2;
    head[u]=tot;
}
int dep[N],now[N];
int bfs()
{
    for(int i=1;i<=T;i++)
    {
        dep[i]=0;
    }
    for(int i=1;i<=T;i++) now[i]=head[i];
    queue<int>q;q.push(S);dep[S]=1;
    while(!q.empty())
    {
        int u=q.front();
        q.pop();
        if(u==T) return 1;
        for(int i=head[u];i;i=e[i].next)
        {
            int v=e[i].to;
            if(!e[i].w||dep[v]) continue;
            dep[v]=dep[u]+1;
            q.push(v);
        }
    }
    return 0;
}
int dinic(int u,int flow)
{
    if(u==T) return flow;
    int rest=flow;
    for(int i=now[u];i;i=e[i].next)
    {
        int v=e[i].to;
        now[u]=i;
        if(!e[i].w||dep[v]!=dep[u]+1) continue;
        int k=dinic(v,min(rest,e[i].w));
        if(!k) dep[v]=-1;
        e[i].w-=k;e[i^1].w+=k;
        rest-=k;
        if(!rest) break;
    }
    return flow-rest;
}
int top,st[N];
bool vis[N][2],instk[N][2];
int match[N];
bool dfs(int u,int w)
{
    if(vis[u][w]) return 0;
    vis[u][w]=1;
    instk[u][w]=1;
    for(int i=head[u];i;i=e[i].next)
    {
        int v=e[i].to;
        if(!e[i].w||e[i].val==-1) continue;
        st[++top]=i;
        int ew=w^e[i].val;
        if(instk[v][ew^1])
        {
            pair<int,int> tmp={v,ew};
            while(tmp!=make_pair(v,ew^1))
            {
                int j=st[top--],nw=e[j^1].to;
                if(nw<=n) match[nw]=j/2;
                tmp=make_pair(nw,tmp.second^e[j^1].val);
            }
            return 1;
        }
        if(dfs(v,ew)) return 1;
        top--;
    }
    instk[u][w]=0;
    return 0;
}
void init()
{
    tot=1;
    for(int i=1;i<=T;i++) head[i]=0;
}
void solve()
{
    scanf("%d%d",&n,&m);
    S=n*2+1;T=n*2+2;
    init();
    for(int i=1;i<=m;i++)
    {
        int x,y,z;
        scanf("%d%d%d",&x,&y,&z);
        add_edge(x,y,1,z);
        add_edge(y,x,0,z);
    }
    for(int i=1;i<=n;i++)
    {
        add_edge(S,i,1,-1);
        add_edge(i,S,0,-1);
    }
    for(int i=n+1;i<=2*n;i++)
    {
        add_edge(i,T,1,-1);
        add_edge(T,i,0,-1);
    }
    int cnt=0;
    while(bfs()) cnt+=dinic(S,1e9);
    if(cnt<n) return printf("-1\n"),void();
    int ans=0;
    for(int i=2;i<=2*m;i+=2)
    {
        if(!e[i].w)
            match[e[i^1].to]=i/2,ans+=e[i].val;
    }
    if(!(ans&1))
    {
        for(int i=1;i<=n;i++) printf("%d ",match[i]);
        putchar('\n');
        return ;
    }
    memset(vis,0,sizeof(vis));
    memset(instk,0,sizeof(instk));
    for(int i=1;i<=n;i++)
    {
        top=0;
        if(dfs(i,0))
        {
            for(int i=1;i<=n;i++) printf("%d ",match[i]);
            putchar('\n');
            return ;
        }
    }
    printf("-1\n");
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        solve();
    }
}

点个赞再走吧。