自动搬运

查看原文

来自洛谷，原作者为

	Zxd2009 **

搬运于2025-08-24 22:54:18，当前版本为作者最后更新于2024-01-31 22:21:05，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题目中给出了 $f(v)$，表示令 $\operatorname{dis}(v, a_i)$ 最小的 $i$，也就是离点 $v$ 最近的关键点 “序号”。或者再换一种说法，我们把每个点的关键点 “序号” 看成它的 “颜色”。

显然，每个 “序号” 只能对应一个关键点，所以每个 “颜色” 里也只有一个关键点。

结合样例，我们发现，颜色相同的点 构成的图一定 连通，否则就无解。

感性理解一下，既然是树，那么任意两点之间绝对存在路径。那么，假如让点 $x$ “走到” 距离自己最近的关键点，如果中途遇到 和自己的关键点不同的点 $y$，那么直接走点 $y$ 的路径肯定更短。所以不存在这种情况。

既然这样，我们就把颜色相同的点看成一个整体，对原树进行 缩点，得到一个新树。

我们发现，某些情况不成立的原因在于，有的点原本应该离自己的关键点更近，现在却离别人的关键点更近。暂且称这种点是错误的。

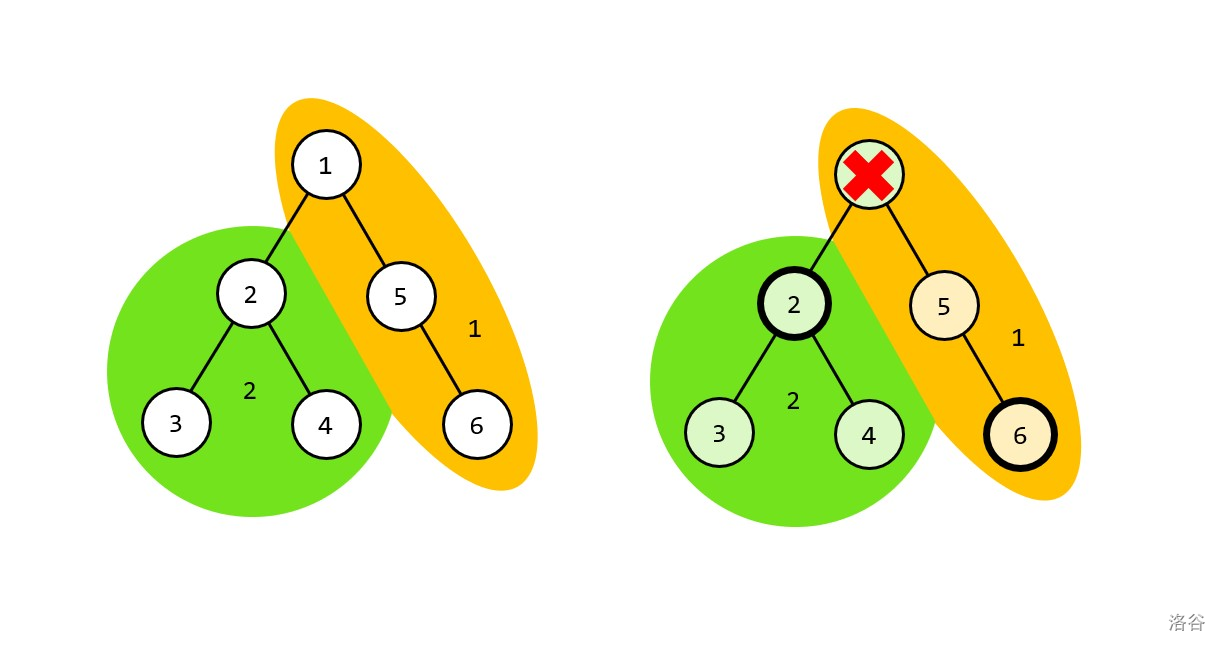
如图，假如选择了点 $2$ 和点 $6$ 作为关键点，那么点 $1$ 就是错误的，它应该离黄色关键点更近，可现在离绿色关键点更近。

能够看出，这种情况下必然有一个 错误的点 在颜色之间的交界处，毕竟如果不在颜色的交界处 而在内部的话，就不符合刚刚那条 “颜色相同的点一定连通” 的性质了。

反过来，如果没有错误的点在颜色的交界处，也就都没有错误的点。那么这种情况就一定成立。

所以，对于每种情况，我们现在需要 判断边界处的点是否正确。

再看一下数据范围：$n \leq 3000$。这意味着我们可以使用 $O(n^2)$ 的算法。

于是，我们可以暴力求出 每个点对的距离 和 每个边界处的点。我们想知道一种情况是否是正确的，只需要枚举所有颜色的边界，检查边界上的点到底离谁更近，就可以了。

接下来，我们就需要引入 树形 DP，定义 f[x][i] 为 “第 $x$ 种颜色，取点 $i$ 作为关键点，（在缩点后的新树上）这棵树及其子树可选择的方案数”。

我们每访问到一个颜色，首先先把这个颜色下面的子树全都访问一遍，然后枚举自己的关键点 $i$、枚举相邻的颜色（子树） $y$、枚举子树的关键点 $j$。

对于子树 $y$，它内部的方案数 是 选择每个关键点的方案数之和。对于树 $x$，它内部的方案数 是 每个子树的方案数之积。答案当然就是 根节点选择每个关键点的方案数之和。

关于时间复杂度：求每个点对的距离是 $O(n^2)$ 的，预处理之后就可以 $O(1)$ 直接使用；每个边界处的点可以在缩点时顺便求出，是 $O(n)$ 的。上面那个 DP 看起来枚举了很多，实际上颜色 $x$ 和颜色内的点 $i$ 乘起来是枚举 $n$ 个点，相邻颜色 $y$ 和颜色内的点 $j$ 乘起来不足 $n$ 个点，所以还是 $O(n^2)$。

如果还不明白可以看代码。

#include <iostream>
#include <cstdio>
#include <vector>
using namespace std;

const int MOD = 998244353;
vector <int> v[3005], s[3005], g[3005];
int T, n, k, x, y, f[3005], dis[3005][3005], jiao[3005][3005];
bool flag, vis[3005];
long long dp[3005][3005], ans;

void suo(int x, int fa)    // 缩点，把旧图缩成新图 
{
	if(flag)  return;    // 如果输入不合法直接退出 
	if(f[x] != f[fa])    // 如果自己和父亲的颜色不同，即遇到交界处 
	{
		g[f[fa]].push_back(f[x]);    // 更新新图 
		g[f[x]].push_back(f[fa]);
		jiao[f[x]][f[fa]] = x;    // 更新交界处数组 
		jiao[f[fa]][f[x]] = fa;
		
		if(vis[f[x]])  flag = true;    // 如果已经访问过这个颜色，输入不合法 
		vis[f[x]] = true;
	}
	s[f[x]].push_back(x);    // 更新颜色内的点编号 
	for(int i = 0; i < v[x].size(); i++)
	{
		if(v[x][i] != fa)  suo(v[x][i], x); 
	}
}
void juli(int root, int x, int fa, int d)    // 在旧树上暴力 dfs 距离 
{
	// root 和 x 是点 
	dis[root][x] = d;    // root 到 x 的距离为 d 
	for(int i = 0; i < v[x].size(); i++)
	{
		if(v[x][i] != fa)  juli(root, v[x][i], x, d + 1);
	}
}

inline bool check(int gx, int vx, int gy, int vy)    // 检查这种情况是否合法 
{
	// gx 和 gy 是颜色，vx 和 vy 是关键点的编号 
	if(gx > gy)  swap(gx, gy), swap(vx, vy);    // 使得 x 颜色编号小于 y 
	int bx = jiao[gx][gy], by = jiao[gy][gx];    // bx 即为 x 与 y 边界处中颜色为 x 的点 
	// 由于距离相同先取编号较小的点，所以第一个是小于等于，第二个是小于 
	return (dis[bx][vx] <= dis[bx][vy]) && (dis[by][vy] < dis[by][vx]);
}
void dfs(int x, int fa)    // 在新树上进行树形 dp，x 和 fa 是颜色种类 
{
	for(int i = 0; i < g[x].size(); i++)
	{
		if(g[x][i] != fa)  dfs(g[x][i], x);    // 先访问每个子树 
	}
	for(int i = 0; i < s[x].size(); i++)    // 枚举自己颜色的关键点（s[x][i]） 
	{
		dp[x][s[x][i]] = 1;
		for(int j = 0; j < g[x].size(); j++)    // 枚举相邻的颜色（g[x][j]） 
		{
			if(g[x][j] == fa)  continue;
			int y = g[x][j];   long long z = 0;    // z 是子树方案数 
			for(int l = 0; l < s[y].size(); l++)    // 枚举子树颜色的关键点（s[y][l]） 
			{
				// 如果 check 成立，z 加上子树方案数，即求和 
				z = (z + dp[y][s[y][l]] * check(x, s[x][i], y, s[y][l])) % MOD;
			}
			// 当前颜色当前关键点的方案数是所有子树方案数的乘积 
			dp[x][s[x][i]] = (dp[x][s[x][i]] * z) % MOD;
		}
	}
}

int main()
{
	scanf("%d", &T);
	for(int t = 1; t <= T; t++)
	{
		scanf("%d%d", &n, &k);
		flag = false, ans = 0;
		for(int i = 1; i <= n; i++)  v[i].clear();
		for(int i = 1; i <= k; i++)  s[i].clear(), g[i].clear(), vis[i] = false;
		
		for(int i = 1; i < n; i++)
		{
			scanf("%d%d", &x, &y);
			v[x].push_back(y);    // 旧图的建图 
			v[y].push_back(x);
		}
		for(int i = 1; i <= n; i++)
		{
			scanf("%d", &f[i]);
		}
		
		suo(1, 0);    // 先进行缩点 
		if(flag)    // 如果输入不合法直接输出 0 
		{
			puts("0");
			continue;
		}
		for(int i = 1; i <= n; i++)
		{
			juli(i, i, 0, 0);    // 暴力枚举距离 
		}
		
		x = f[1];
		dfs(x, 0);    // 进行树形 dp 
		for(int i = 0; i < s[x].size(); i++)
		{
			// 答案为新树的根节点每种关键点方案数之和 
			ans = (ans + dp[x][s[x][i]]) % MOD;
		}
		printf("%lld\n", ans);
	}
	return 0;
}

如果有错欢迎讨论交流