自动搬运

查看原文

来自洛谷，原作者为

	聪明王必胜 永恒的王~

搬运于2025-08-24 21:19:51，当前版本为作者最后更新于2017-10-30 20:36:00，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

##作为一个动归初学者，感觉各位大佬的题解太过麻烦（其实是我看不懂）

#我领悟到了真正简单的方法，相信蒟蒻们也能看懂（莫名自信）

因为是从上方和从下方传纸条，为了方便，我们相当于从左上角连续传两张纸条，路径不重复，效果相同。

从左上来看的话就只能向右或向下传纸条。

##那么两张纸条在过程中就一定在一条斜线上，而在一条斜线上纵坐标与横坐标相加相等。

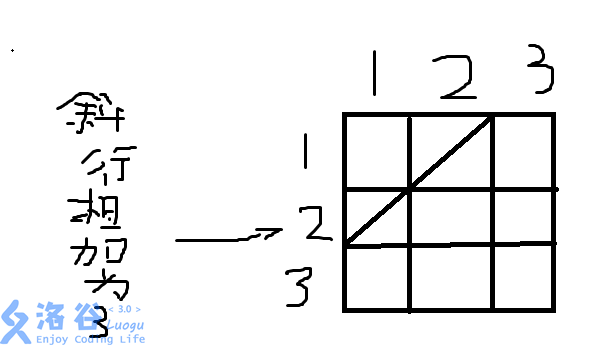在如图的斜线中，两个点的和都为3.

首先重要的就是三维F数组。

第一维度维护的是在传的过程中纵坐标与横坐标的和。

#在同一斜线上，剩下表示两个点的从坐标就可以表示这两个点的位置。

第二维度维护的是相对在左边的点的纵坐标。

第三维度维护的是相对在右边的点的纵坐标。

当查询一个情况时，只有四种情况可以到他

F[sum][i][j]=max{F[sum-1][i][j]+F[k-1][i][j-1]+F[k-1][i-1][j]+F[k-1][i-1][j-1]；

最后再加上a数组里存的两个点的好感度即可

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
const int maxn=60;
int a[maxn][maxn];
int F[2*maxn][maxn][maxn];
int main()
{
  int m,n;
  scanf("%d%d",&m,&n);
  for(int i=1;i<=m;i++)
    for(int j=1;j<=n;j++)
      scanf("%d",&a[i][j]);
  //F[sum][i][j]=max{F[sum-1][i][j]...
  memset(F,-1,sizeof(F));//赋初值为-1 (原因在后面） 
  F[2][1][1]=0;//最初的点，在左上角，好感度为0 
  for(int k=3;k<m+n;k++)
    for(int i=1;i<n;i++)
      for(int j=i+1;j<=n;j++)
      {
        int s=F[k][i][j];
        if(F[k-1][i][j]>s)s=F[k-1][i][j];
        if(F[k-1][i-1][j]>s)s=F[k-1][i-1][j];
        if(F[k-1][i][j-1]>s)s=F[k-1][i][j-1];
        if(F[k-1][i-1][j-1]>s)s=F[k-1][i-1][j-1];
        if(s==-1)continue;//当s为-1时，说明四种情况都不能到该点，故不存在。 
        F[k][i][j]=s+a[k-i][i]+a[k-j][j];//该点的值为最大的前一个值与当前F[k][i][j]表示两点的值的和。 
      }
  printf("%d",F[m+n-1][n-1][n]);//因为i永远小于j，所以右下角的点不会求到，
  //但是到右下角只有一种情况，就是在右下角的上面和右下角的左边，直接输出就好了。 
  return 0;
 }