1 条题解
-
0
自动搬运
来自洛谷,原作者为

小胖同学
高二蒟蒻,在线躺平搬运于
2025-08-24 22:53:58,当前版本为作者最后更新于2023-04-05 12:10:49,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
「HCOI-R1」孤独的 sxz - 题解
官方题解
Easy Version
【设】
表示 sxz 坐在 时的曼哈顿距离之和。
【分析】
下图中黄色格子为同学,红色格子为 sxz 。黄色格子里的数为此格子对于 sxz 的曼哈顿距离。
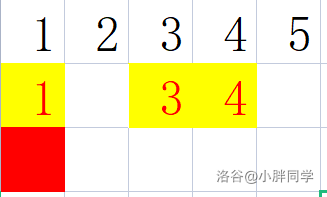
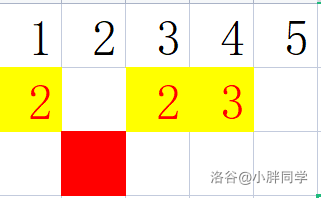
观察可以发现当 sxz 从 移动到 时:
矩阵内 的曼哈顿距离 ; 的曼哈顿距离 。
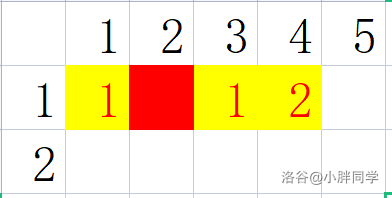
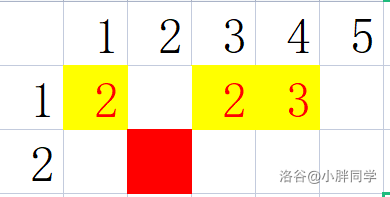
同理当 sxz 从 移动到 时:
矩阵内 的曼哈顿距离 ;
的曼哈顿距离 。
【递推式】
注: 代表第 行第 列是否有同学。
$cnt_h = \sum _ {p = 1} ^ {n} \sum _ {q = 1} ^ {j - 1} a[i][j]$
$cnt_t = \sum _ {p = 1} ^ {n} \sum _ {q = j} ^ {m} a[i][j]$
$cnt_l = \sum _ {p = 1} ^ {i - 1} \sum _ {q = 1} ^ {m} a[i][j]$
$cnt_r = \sum _ {p = i} ^ {n} \sum _ {q = 1} ^ {m} a[i][j]$
【实现】
预处理每一行和每一列的同学数。
统计 的值。
拓广。
Hard Version
观察式子可以发现,对于列而言,相邻的两人间的的曼哈顿距离一定是单调的,行同理。
考虑 预处理 的值。
计算 , $(x_i - 1 , y_i)(x_i + 1 , y_i)(x_i , y_i - 1)(x_i , y_i + 1)$ 和
转移乘上距离 $f[x_i][y_i] = f[x _ {i - 1}][y _ {i - 1}] + cnt_h \times (x_i - x_{x - 1}) - cnt_t \times (y_i - y_{i - 1})$ 就可以了。
- 1
信息
- ID
- 8288
- 时间
- 1000ms
- 内存
- 512MiB
- 难度
- 4
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
