自动搬运

查看原文

来自洛谷，原作者为

	raincs 比起1e9+7，我更熟悉0x3f

搬运于2025-08-24 21:18:15，当前版本为作者最后更新于2025-05-10 09:37:17，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

解题过程

先读题，给定 $n$ 个宽为 $1$ 的矩形，每个矩形的高各不相同。将它们拼在一起，要求在从中剪出一块最大的矩形纸片。
我们很自然可以想到枚举左右起始位置，在枚举中间的位置来计算当前区间内的最大矩形长度，再来更新答案。

#include<bits/stdc++.h>
using namespace std;
int h[1000001];
int main(){
	int n;
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>h[i];
	}
	int maxn=0;
	for(int i=1;i<=n;i++){
		int m=1e9+1;
		for(int j=i;j<=n;j++){
			for(int k=i;k<=j;k++){
				m=min(m,h[k]);
			} 
			maxn=max(maxn,m*(j-i+1));
		}
	}
	cout<<maxn<<endl;
	return 0;
}

结果……$30$ 分
我们可以发现该解法的时间复杂度为 $O(n^3 )$。 所以我们得换一种方法来写。 我们可以先假设矩形长度递增，那么我们该如何做？
很显然，我们可以尝试将当前的矩形的高度作为最后矩形的高度，并将该矩形的宽一直延伸到右边界，再算出矩形的面积用来更新答案。
所以我们看回这道题，我们可以利用上面的结论，如果下一个矩形的高度比上一个小，那么该矩形想与前面的矩形拼成一个更大的矩形，那么之前的矩形高于当前矩形的面积就没有任何用处了(如下图中打叉的部分)。

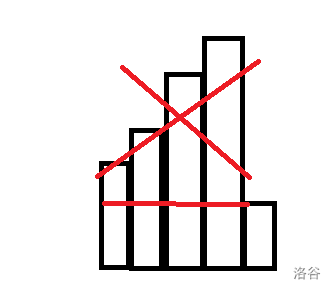
所以我们就可以用到一种算法来解决这种问题————单调栈。
我们只需要建立一个栈，用来维护一个高度始终单调的序列，这样我们就可以解决这个问题了。
我们先从左到右依次扫描每个矩形，如果当前的矩形高度高于栈顶矩形，就让其进栈；否则就不断取出栈顶，直至栈为空或栈顶矩形的高度比当前矩形小。出栈过程中我们累加弹出矩形的宽度，并且在每次弹出时，就用其高度乘以累加的宽度去更新答案。出栈结束后，我们再把一个高度为当前矩形高度、宽度为累加值的矩形入栈。注意，结束后，要将栈中剩下的矩形依次弹出，采用上面相同的方法来更新答案。所以我们可以增加一个高度为 $0$ 的矩形，避免再扫描结束后有剩余矩形。

AC_code

数组模拟

#include<bits/stdc++.h>
using namespace std;
#define int long long
int a[1000001];
int s[1000001];
int w[1000001];
int n;
signed main(){
	int p=0,ans=0;
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i]; 
	a[n+1]=0; 
	for(int i=1;i<=n+1;i++){
		if(a[i]>s[p]){
			s[++p]=a[i];
			w[p]=1;
		}
		else{
			int width=0;
			while(s[p]>a[i]){
				width+=w[p];
				ans=max(ans,(long long)width*s[p]);
				p--;
			}
			s[++p]=a[i];
			w[p]=width+1;
		}
	}
	cout<<ans<<endl;
	return 0;
}

STL

#include<bits/stdc++.h>
using namespace std;
struct node{
	int h,w;
};
stack<node>s;
long long a[1000001];
long long ans=0;
int main(){
	int n;
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i];
	a[n+1]=0;
	for(int i=1;i<=n+1;i++){
		long long width=0;
		while(!s.empty() && a[i]<s.top().h){//单调递增
			width=width+s.top().w;
			ans=max(ans,width*s.top().h);
			s.pop();
		}
		s.push( (node){a[i],width+1} );
	}
	cout<<ans<<endl;
	return 0;
}