自动搬运

查看原文

来自洛谷，原作者为

	qhr2023 **

搬运于2025-08-24 21:17:30，当前版本为作者最后更新于2025-03-13 22:28:45，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

solution

一道构造。

先假设已经有了 $n$ 个点的解，考虑推广到 $n+2$ 个点。

因为 $n$ 个点内部是合法的，令 $n+1$ 和 $n+2$ 到这 $n$ 个点的距离及 $n$ 个点到 $n+1$ 和 $n+2$ 距离都不超过 $2$ 即可。

我们可以从 $n+2$ 到 $n$ 个点都连一条边，$n$ 个点每个点都连一条到 $n+1$ 的边，$n+1$ 再连一条到 $n+2$ 的边，这样就是一种合法的 $n+2$ 的方案了。

如下图，黑点是 $n$ 个点，红色是新加的 $2$ 个点，我们先不管心 $n$ 个点内部怎么连。

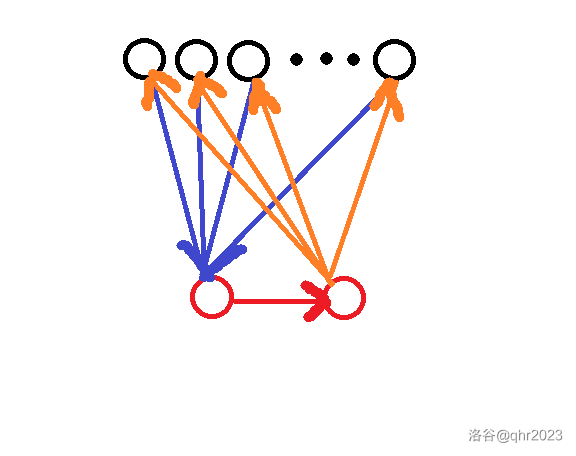
所以我们知道，只要 $n$ 个点有解，那 $n+2$ 个点也一定有解。

故只要找到有解的最小奇数和偶数即可，$1$ 个点时显然成立，所以奇数都有解，而最小的偶数通过手算是 $6$。这样就可以构造所有 $1+2k$ 和 $6+2k$ 的解了，$k$ 是非负整数。

实现方面，对于奇数，从 $2$ 开始执行上述的连边即可；对于偶数，可以把前 $6$ 个点的边连完，从 $7$ 开始执行上述连边即可。下图是 $n=6$ 的解。

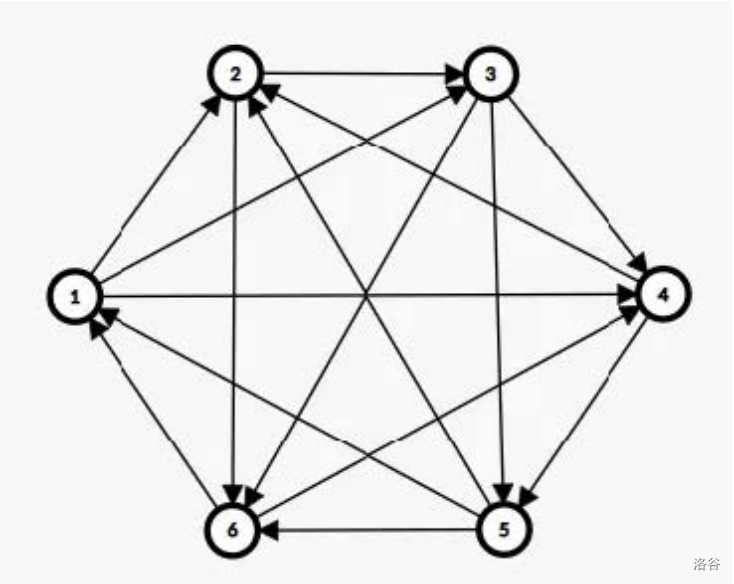
code

#include <bits/stdc++.h>
using namespace std;
int n, a[505][505];
int main () {
	cin >> n;
	if (n==2||n==4) {
		puts("NO");
		return 0;
	}
	puts("YES");
	if (n%2==0) 
		a[1][2]=a[1][3]=a[1][4]=1,
		a[2][3]=a[2][5]=a[2][6]=1,
		a[3][4]=a[3][5]=a[3][6]=1,
		a[4][5]=a[4][2]=a[5][6]=a[5][1]=a[6][1]=a[6][4]=1;
	for (int i=(n%2?2:7); i<=n; a[i][i+1]=1, i+=2)
			for (int j=1; j<i; ++j)
				a[j][i]=a[i+1][j]=1;
	for (int i=1; i<=n; ++i, cout << '\n')
		for (int j=1; j<=n; ++j)
			cout << a[i][j] << ' ';
	return 0;
}