自动搬运

查看原文

来自洛谷，原作者为

	2021CHD 这个家伙很懒，什么也没有留下？

搬运于2025-08-24 21:17:06，当前版本为作者最后更新于2025-01-02 11:19:26，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题目大意

问字符串 $S$ 是否可以被划分为 $n(n>1)$ 个非空子串 $S_1,S_2,\dots,S_n$，满足对于所有 $1\le i\le n$，有 $S_i=S_{n-i+1}$ 或 $S_i=\text{rev}(S_{n-i+1})$，若可以，求出 $n$ 的最大值。

其中 $\text{rev}(T)$ 表示将字符串 $T$ 反转得到的结果。

• $1\le |S|\le10^4$，其中 $|S|$ 表示字符串 $S$ 的长度。

题解

首先可以将 $n>1$ 的限制解除再求出 $n$ 的最大值，如果最大值是 $1$，就是无解，否则就是有解。

第一个显然的观察是 $|S_i|=|S_{n-i+1}|$。

首先可以考虑到，其实题目中给出的 $S_i=\text{rev}(S_{n-i+1})$ 的条件其实是无用的，原因见下图。

所有的 $S_i=\text{rev}(S_{n+1-i})$ 就可以表示成 $|S_i|$ 对相等的字符串，而在这个过程中，$n$ 不会减小。

（另外，如果 $n$ 是奇数，那 $S_{\frac{n+1}{2}}$ 始终和自身相等，所以不用考虑 $S_{\frac{n+1}{2}}=\text{rev}\left(S_{\frac{n+1}{2}}\right)$ 这种情况）

所以现在只需考虑对所有的 $i$ 都满足 $S_i=S_{n-i+1}$ 的情况。

容易想到一个贪心：每次从两边贪心地选取最短的一个合法的串，直接把这个串选上并计入答案。如果选中的两个串有重叠部分，说明只能把最后一个串放在中间，答案就会是奇数。

实现是容易的，但是很多人可能忽略了一个问题：为什么这样是对的呢？

考虑一个位置，如果在这个位置上有两种可转移的串，下面这两张图说明了选短的串一定由于选长的串：

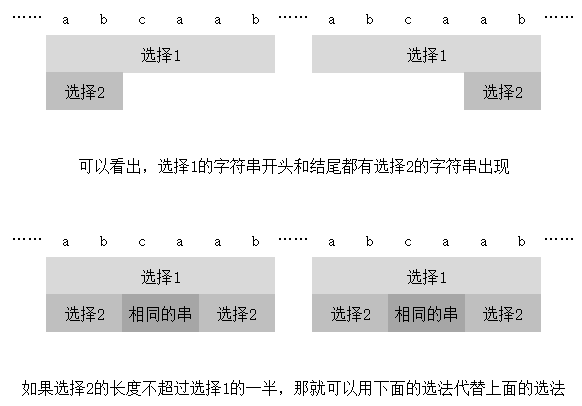
此时 $n$ 会增加，而且选择二包含了选择一，所以选择二更优。

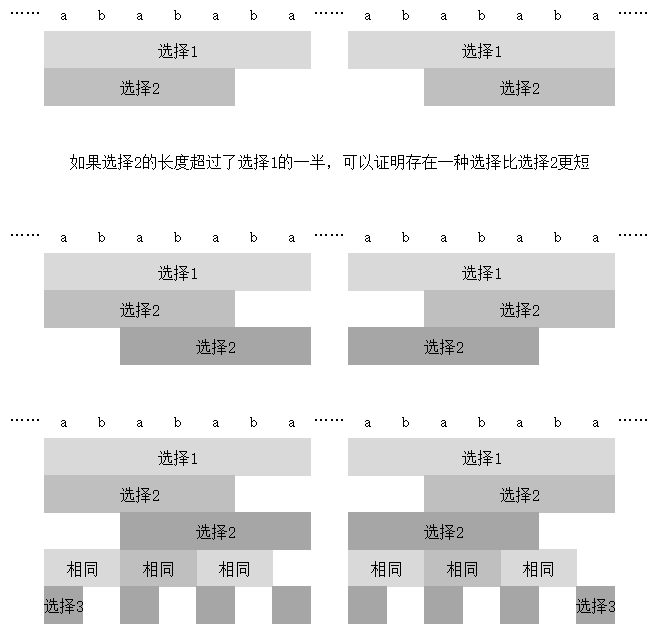
具体地，如果选择一的长度为 $L_1$，选择二的长度为 $L_2>\frac{L_1}{2}$，那一定有一种长为 $(L_1-1)\bmod(L_1-L_2)+1$ 的选择。

另外，如果选择 1 是选择最中心的整个串，那显然不可能比选择 2 更优。

所以我们可以放心地说这个贪心是对的。

贴上代码和 AC 记录。

#include<cstdio>
#include<cstring>
using namespace std;
int n,i,j,ll,len,ans;
char s[11000];
main()
{
	scanf("%s",s+1);
	len=strlen(s+1);
	ll=1;
	for(i=1;i<=len;i++)
	{
		for(j=ll;j<=i;j++)
		if(s[j]!=s[len-i+j-ll+1])
		break;
		if(j>i)
		{
			ll=i+1;
			if(i*2<=len)
			ans=ans+2;
			else
			ans++;
		}
		if(ll*2-1>len)
		break;
	}
	if(ans==1)
	printf("NO");
	else
	printf("YES\n%d",ans);
}

后记

随便开了一道题，发现是黄的，花了几分钟做了出来，感觉是一道好题。

打开题解区，发现上面写着“算法分析：好像没有。”

……

于是我决定把证明补上。