自动搬运

查看原文

来自洛谷，原作者为

	ShiRoZeTsu AFOed

搬运于2025-08-24 21:16:19，当前版本为作者最后更新于2024-05-20 17:38:17，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

Source & Knowledge

2024 年 5 月语言月赛，由洛谷网校入门计划/基础计划提供。

题目大意

给定一个 $n \times n$ 的方阵，请你取一行，一列，或者与对角线平行的一条只经过格点的直线，满足经过的数字和最大。

题目分析

首先，开一个二维数组 a 来存储方阵上的数字：

int a[2005][2005];

然后开两个变量 ans 和 res。 ans 代表最终答案，初始要赋值成一个很小的负数（比如 $-10^{18}$）；res 代表一个临时变量，用来统计某一行、某一列或某一斜线上的数字和。注意数据范围，要使用 long long 类型：

long long res, ans = -1e18;

接下来考虑求出答案。取一行、一列的情况是好写的。对于取一行的情况，我们可以循环枚举每一行，然后分别算出每一行的数字和，用数字和去更新答案。写法如下：

for(int i = 1; i <= n; i++) {
    res = 0;
    for(int j = 1; j <= n; j++)
        res += a[i][j];
    ans = max(ans, res);
}

取一列的情况同理，枚举列即可：

for(int i = 1; i <= n; i++) {
    res = 0;
    for(int j = 1; j <= n; j++)
        res += a[j][i];
    ans = max(ans, res);
}	

接下来考虑如何求与对角线平行的情况。这里我们首先需要了解一个知识点：

• 考虑从左上到右下的对角线。对于任意一条与这个对角线平行的直线，其经过的所有格子的行数与列数之差一定相同。

我们这里画图来解释一下。

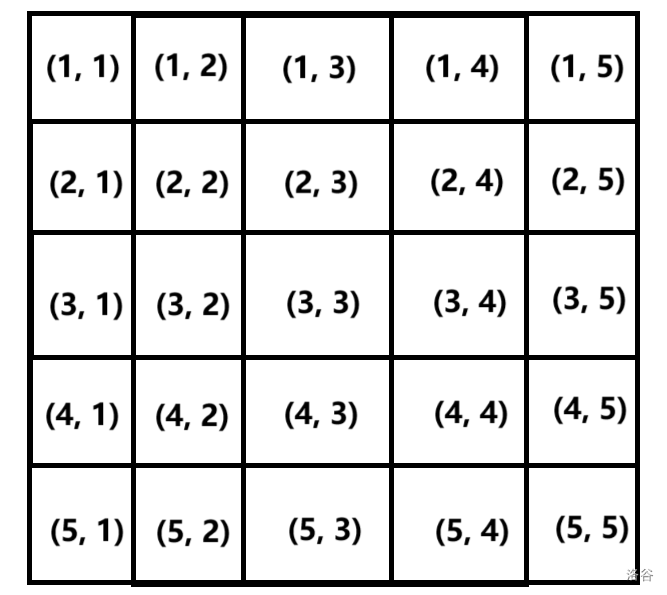
首先，这是一个 $5 \times 5$ 的方阵。我们随便取一条从左上到右下的满足条件的斜线：

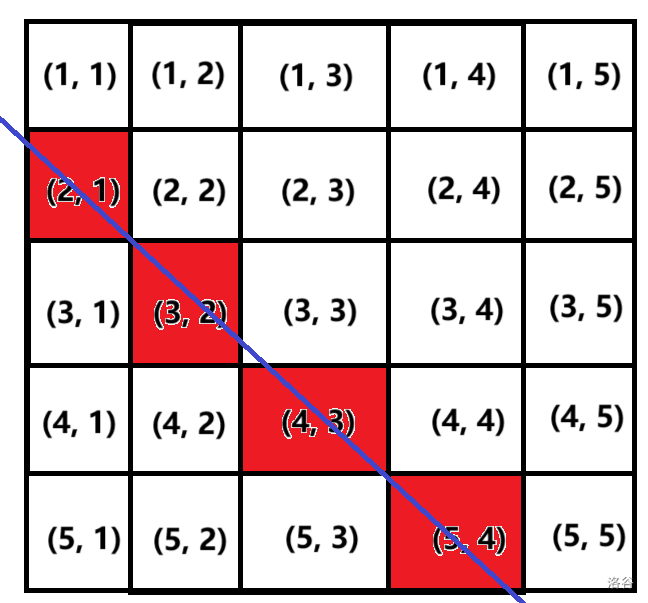
不难发现，$(2, 1), (3, 2), (4, 3), (5, 4)$ 都满足行数 $-$ 列数 $= 1$。大家也可以试试其它斜线，可以发现都满足上面的规律。

• 考虑从右上到左下的对角线。对于任意一条与这个对角线平行的直线，其经过的所有格子的行数与列数之和一定相同。

我们同样画图来解释一下。

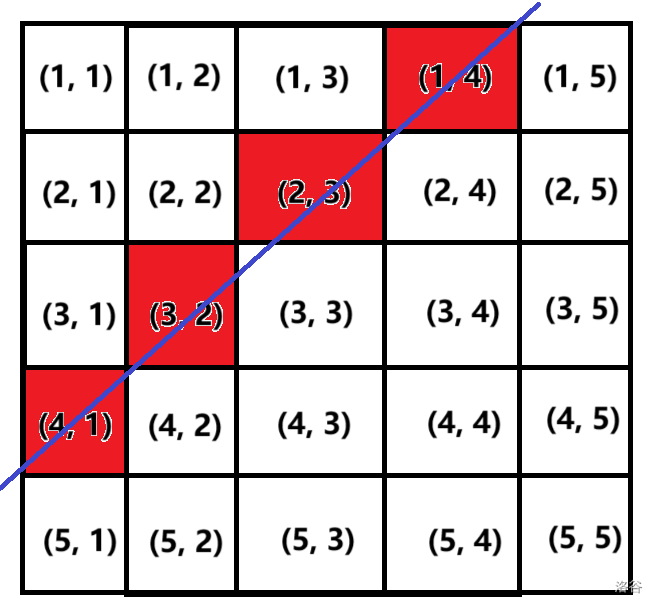
不难发现，$(1, 4), (2, 3), (3, 2), (4, 1)$ 都满足行数 $+$ 列数 $= 5$。大家也可以试试其它斜线，可以发现都满足上面的规律。

因此，对于从左上到右下的斜线，我们可以选择枚举行数与列数的差，这样就相当于枚举了这条斜线。然后将斜线上的数字都加起来，去更新答案：

//这里 i 代表正在枚举的行数与列数的差（左上到右下）
//行和列的最小值都是 1，最大值都是 n，所以这个差值最小就是 1-n，最大是 n-1
for(int i = 1-n; i <= n-1; i++) {
    res = 0;
    //然后枚举这条线上所有格子的行数 j
    //那么此时列数就等于 j-i
    for(int j = 1; j <= n; j++)
    //这里 j-i 还要判断范围，是因为要保证这个格子不能出界
        if(1 <= j-i && j-i <= n) res += a[j][j-i];
    ans = max(ans, res);
}

从右上到左下的斜线也类似：

//这里 i 代表正在枚举的行数与列数的和（右上到左下）
//行和列的最小值都是 1，最大值都是 n，所以这个和值最小就是 2，最大是 n+n
for(int i = 2; i <= n+n; i++) {
    res = 0;
    //然后枚举这条线上所有格子的行数 j
    //那么此时列数就等于 i-j
    for(int j = 1; j <= n; j++)
        //这里 i-j 还要判断范围，是因为要保证这个格子不能出界
        if(1 <= i-j && i-j <= n) res += a[j][i-j];
    ans = max(ans, res);
}

最后输出答案即可：

cout << ans << '\n';

视频讲解