二叉树的遍历

0
15011418730 LV 7 @ 2025-8-24 21:14:08
自动搬运

查看原文

来自洛谷，原作者为

ShanCreeperPro
DILL QQTeam：746219450

搬运于2025-08-24 21:14:07，当前版本为作者最后更新于2022-07-12 22:06:40，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

B3642 二叉树的遍历題解

管理员注：

阅读本文章前，请先阅读 $\ \texttt{ShanCreeper}$ B 题库题解的声明，并了解由于课程需要不展示 C++ 代码。

如需系统学习相关知识点请报名【洛谷-基础算法计划】

首先你要知道什么是树。

树形结构：
- 不仅能表示数据间的指向关系；
- 还能表示出数据层次关系；
例如一棵树：

不好意思，放错了，是这棵树：

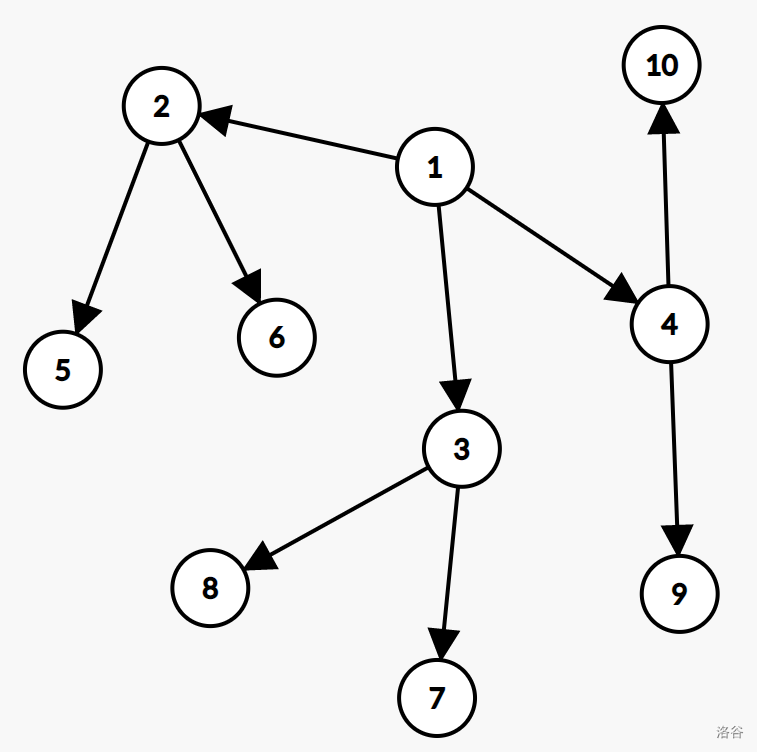
这种结构成为树，树有以下概念：
- 结点：这颗树上的每一个数字都是一个结点；
- 根结点：这棵树的最顶端叫做根结点；
- 叶子节点：除了根结点的节点都是叶子结点；
- 父结点：一个结点能指向另一个结点的结点叫做父结点；
- 兄弟结点：若干个结点同时拥有同个父结点的结点叫做兄弟结点；
- 子结点：父结点指向的那个结点叫做子结点；
- 祖先：一个结点的父结点及其所有父结点都为该结点的祖先；
- 子树：以该结点的子结点为根结点的树叫做子树。
可能讲的有点抽象，大概能理解就行了。

那么这道题问的是二叉树，那什么是二叉树呢？

二叉树是树的一种，是每个结点都不超过两个子结点的树。

二叉树的每个结点，可能有：
- 左子结点和左子树；
- 右子结点和右子树；
好接下来讲这道题。

对于任意给定结点，可以访问该结点本身、遍历左子树、遍历右子树。

我们就可以分为前序遍历、中序遍历、后序遍历。

前序遍历（先序遍历）：
- 先访问根节点；
- 然后访问左子树；
- 最后访问右子树。
例如这棵：

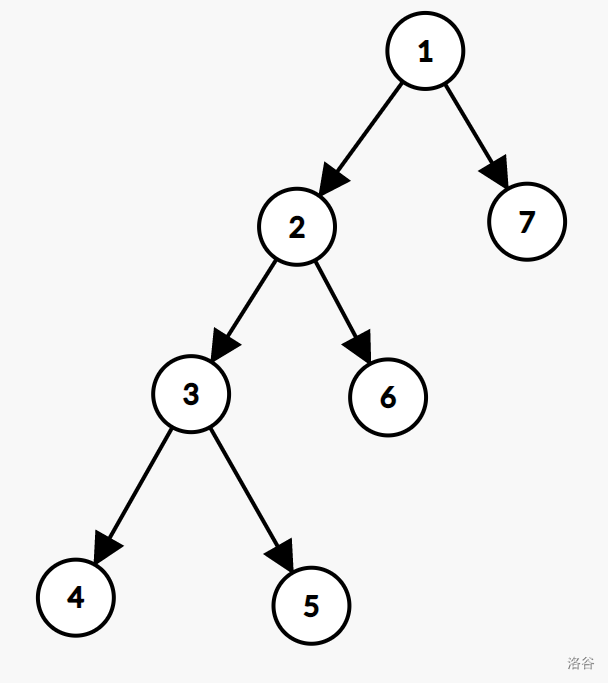
我们按照根左右的顺序遍历：
- 先访问根结点，1；
- 访问左子树，即以 2 为根结点的树：
  
  先访问根结点，2；
  
  访问左子树，即以 3 为根结点的树：
  
  先访问根结点，3；
  
  访问左子树，即以 4 为根结点的树：
  
  先访问根结点，4；
  
  无左子树、无右子树，该树遍历完成。
  
  访问右子树，即以 5 为根结点的树：
  
  先访问根节点，5；
  
  无左子树、无右子树，该树遍历完成。
  
  根左右遍历完成，该树遍历完成。
  
  访问右子树，即以 6 为根结点的树：
  
  先访问根结点，6；
  
  无左子树、无右子树，该树遍历完成。
  
  根左右遍历完成，该树遍历完成。
- 访问右子树，即以 7 为根结点的树：
  
  先访问根结点，7；
  
  根左右遍历完成，该树遍历完成。
就是这么遍历的，所以前序为 $1 \ 2 \ 3 \ 4 \ 5 \ 6 \ 7$ 。

中序遍历为：先遍历左子树，然后为根结点，最后遍历右子树。

后序遍历为：先遍历左子树，然后遍历右子树，最后为根结点。

所以（嘿嘿嘿我放非 C++ Code）：

前序遍历：
- 首先输出根结点，即 $x$ ；
- 然后遍历左子树，即 $\text{tree}_i.\text{left}$ ；
- 最后遍历右子树，即 $\text{tree}_i.\text{right}$ ；
```
func pre_order(x int){
	fmt.Print(x)
	if tree[x].left==0{
		pre_order(tree[x].left)
	}
	if tree[x].right==0{
		pre_order(tree[x].right)
	}
}
```
注意，当左子树和右子树存在时，才能继续递归。

中序遍历：
- 首先遍历左子树；
- 然后输出根结点；
- 最后遍历右子树；
```
func in_order(x int){
	if tree[x].left==0{
		in_order(tree[x].left)
	}	
	fmt.Print(x)
	if tree[x].right==0{
		in_order(tree[x].right)
	}
}
```
后序遍历：
- 首先遍历左子树；
- 然后遍历右子树；
- 最后输出根结点；
```
func post_order(x int){
	if tree[x].left==0{
		post_order(tree[x].left)
	}
	if tree[x].right==0{
		post_order(tree[x].right)
	}
	fmt.Print(x)	
}
```