自动搬运

查看原文

来自洛谷，原作者为

	Hamer_sans 迷路ing

搬运于2025-08-24 21:13:53，当前版本为作者最后更新于2021-08-26 11:14:47，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

$Update$

第一次修改：$10$ 月 $4$ 日调整代码

题目大意：

求点双连通分量有多少个，但是特别的，在每一个点双连通分量中的节点要按从大到小的去排序，对于每一个点双连通分量要按字典序进行排序，其他的就和一个板子任何的区别。

什么是点双连通分量？

首先我们要先知道什么是时间戳，时间戳就是深度优先遍历的过程中，给依次被访问的节点进行整数标记,这种标记就被称为时间戳，记为 $dfn$。

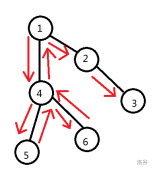
就比如说这幅图，红箭头指的方向和顺序就是深度优先遍历的顺序，如果假设 $1$ 根节点，深度优先遍历从 $1$ 开始，所以我们按照其顺序就可以得到 $dfn$ 数组的值，如 $dfn_{1}=1$，$dfn_{4}=2$，$dfn_{5}=3$ ... $dfn_{3}=6$。

然后我们需要知道什么是搜索树，在无向连通图中任选一个节点进行深度优先遍历，每个点只访问一次。所有发生递归的边 $(x,y)$ 所构成的一棵树，我们把它称做“无向连通图的搜索树”。

最后还有一个东西，叫做追溯值 $low$，我们设 $subtree(x)$ 表示搜索树中以 $x$ 为根节点的子树，$low_{x}$ 定义为以下节点的时间戳的最小值:

1.$subtree(x)$ 中的节点。

2.通过 $1$ 条不在搜索树上的边，能够达到 $subtree(x)$ 的节点。

最后的最后还有一个东西，它的名字叫做割点，什么是割点呢？在无向连通图中，如果将这个节点和它与其它点的连删除后，这时无向连通图还会被分成若干个的无向连通图，于是我们就把这个点叫做割点。那如何来判断这个点是否是割点呢？首先，割点不能为搜索树的根节点，并且割点至少要有两个子节点。比如说这幅图： $x$ 就是割点。

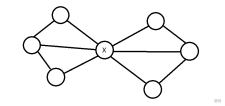
好的，现在终于可以开始正题了。点双连通分量，也就是 v-DCC ，它的定义是一张不存在割点的无向连通图，那我们怎么求点双连通分量呢？我们用一个栈来储存点双连通分量的节点，在用利用时间戳实现的 Tarjan 算法对这个栈进行维护。当一个元素第一次被访问时，就将这个元素进栈，当 $dfn_{x} \le low_{y}$ 成立时，就开始弹出之前进栈的元素，并且记录下来，直到将节点 $y$ 弹出为止，这些弹出的元素一起构成一个点双连通分量。

代码

#include<bits/stdc++.h>
using namespace std;
const int N=5e4+5,M=3e5+5;
int ver[M],head[N],ne[M],tot;
int n,m;
int dfn[N],low[N],timestamp;
bool cut[N];
int root;
int stk[N],tt;
int cnt;
vector<int> dcc[N];
void add(int x,int y){
	ver[++tot]=y;
	ne[tot]=head[x];
	head[x]=tot;
	return;
}
bool cmp(vector<int> x,vector<int> y){
	int len=min(x.size(),y.size());
	for(register int i=0;i<len;++i){
		if(x[i]<y[i]) return 1;
		else if(x[i]>y[i]) return 0;
	}
	return x.size()<y.size();
}
void tarjan(int x){
	dfn[x]=low[x]=++timestamp;
	stk[++tt]=x;
	for(register int i=head[x];i;i=ne[i]){
		int y=ver[i];
		if(!dfn[y]){
			tarjan(y);
			low[x]=min(low[x],low[y]);
			if(low[y]>=dfn[x]){
				cnt++;
				int d;
				do{
					d=stk[tt--];
					dcc[cnt].push_back(d);
				}while(d!=y);
				dcc[cnt].push_back(x);
			}
		}else low[x]=min(low[x],dfn[y]);
	}
	return;
}
int main(){
	scanf("%d%d",&n,&m);
	for(register int i=1;i<=m;++i){
		int x,y;
		scanf("%d%d",&x,&y);
		if(x==y) continue;
		add(x,y);
		add(y,x);
	}
	for(register int i=1;i<=n;++i){
		if(!dfn[i]) root=i,tarjan(i);
	}
	for(register int i=1;i<=cnt;++i) sort(dcc[i].begin(),dcc[i].end());
	sort(dcc+1,dcc+cnt+1,cmp);
	printf("%d\n",cnt);
	for(register int i=1;i<=cnt;++i){
		for(register int j=0;j<dcc[i].size();++j){
			printf("%d ",dcc[i][j]);
		}
		puts("");
	}
	return 0;
}

本题解参考资料书《算法竞赛进阶指南》，蒟蒻写题解不易，求点赞。