自动搬运

查看原文

来自洛谷，原作者为

	strcmp 每一个不曾起舞的日子，都是对生命的辜负

搬运于2025-08-24 21:13:51，当前版本为作者最后更新于2022-02-14 14:41:34，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

看见没有 ISAP 的题解，蒟蒻刚学 ISAP 就贡献一个吧。

步入正题

1.ISAP 算法是什么？

是一种计算网络流的高效最短增广路算法，它其实是优化版的最短增广路算法，最短增广路算法即 EK 算法。

2.Dinic 算法和 ISAP 算法的区别？

Dinic 算法每次 DFS 后，会从源点 $s$ 到汇点 $t$ 进行一次 BFS 来维护层次图。但 ISAP 算法从始至终只进行一次从汇点 $t$ 到源点 $s$ 的 BFS，但 DFS 的时候要同时维护结点的深度。

3.ISAP 算法具体有哪些步骤？

1.首先，从汇点 $t$ 到源点 $s$ 进行一次 BFS。

2.然后，每次沿着深度连续的结点进行增广，然后更新路径上的结点深度。

3.如果某个深度不存在或者源点 $s$ 的深度大于等于结点个数 $n$ 时结束，否则转步骤 2（不是转步骤 1）

ISAP 的神奇之处在于它不用再进行 BFS 就能维护层次图。

首先是初始化历程，这里使用链式前向星进行存图。

#define inf 1000000000000000
#define V 20010
#define E 500010
typedef long long int ll;
struct edge {
public:
	int to, next;
	ll capa;
};
int cnt = 0, head[V]; int n, m; vector<edge>node(E);
inline void add(int fir, int nxt, ll w) {
	node[cnt].to = nxt;
	node[cnt].capa = w;
	node[cnt].next = head[fir];
	head[fir] = cnt; ++cnt;
}
int s, t, dep[V], gap[V], cur[V]; queue<int>que; ll sum = 0;
inline void initing() {
	memset(dep, -1, (n + 1) * sizeof(int));
	memcpy(cur, head, (n + 1) * sizeof(int));
}

其中有三个新数组：分别是 $dep$, $gap$ 和 $cur$。

$cur$ 用于“当前弧优化”，将于后面介绍，那 $dep$ 和 $gap$ 是指什么呢？

在图 $G=(V,E)$ 中， $dep$ 可以对应于一个新函数 。

$$\operatorname{dep}(u),u \in V$$

它代表这个结点的深度。你先不要纠结深度是什么，下面会讲。

同样， $gap$ 也可以对应一个新函数。

$$\operatorname{gap}(d),d \in \operatorname{deep(u)},u \in V $$

它代表这个深度对应的结点数。

那它们有什么用呢？

先放图。

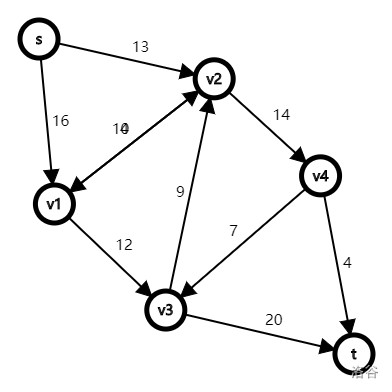
因为工具的限制，反向弧以及结点 $v1$ 和 $v2$ 之间的重边无法正常展示。

ISAP 会先用 BFS 造层次图。注意是从汇点 $t$ 开始 BFS ，不是从源点 $s$ 开始的。

下面是 BFS 后图的状态。

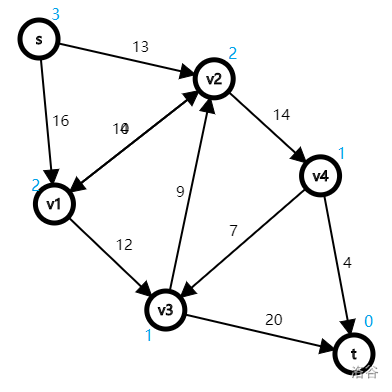
具体过程如下：

1.将汇点 $t$ 入队。

2.遍历队首结点每个出边，将边对应的结点入队，入队的结点深度为队首结点深度 +$1$

3.将队首结点出队，如果队列不为空，转步骤 $2$，否则直接结束

注意，这里有一个坑点：

if (dep[ito] == -1)

BFS 的时候一定只通过深度判定是否遍历过，不能判定边权大小，因为初始反向边是没有边权的，而我们因为是从汇点 $t$ 开始 BFS 的，所以要通过反向边才能到达源点 $s$。

代码如下：

void bfs() {
	int fro, i, ito;
	que.push(t); deep[t] = 0; ++gap[deep[t]];
	while (!que.empty()) {
		fro = que.front(); que.pop();
		for (i = head[fro]; i != -1; i = node[i].next) {
			ito = node[i].to;
			if (deep[ito] == -1) {//不要特判边权为 0
				deep[ito] = deep[fro] + 1;
				que.push(ito);
				++gap[deep[ito]];//别忘了给 gap 加 1
			}
		}
	}
}

有了这个深度有什么用呢？能让我们找到的增广路一定是最短增广路。

怎么走呢？

首先给 DFS 两个参数：“当前结点 $u$” 和 “从 $s$ 到 $u$ 增广路径上最小边权 $flow$”。再加上一个变量：“当前结点已经增广出去的流量 $used$ ”。

记住下面几个原则：

1.从源点 $s$ 开始 DFS。

2.只沿着深度连续的增广路径增广，只通过边权不为 $0$ 的边增广。

3.当 $used$ 等于 $flow$ 时及时停止。

4.当增广后 $used$ 小于 $flow$ 时将结点 $u$ 的深度 +$1$。

先看看代码感受一下。

ll dfs(int u, ll flow) {
	if (u == t || flow == 0)return flow; ll used = 0;
	for (int i = cur[u]; i != -1; i = node[i].next;) {
		cur[u] = i;
		if (dep[u] == dep[node[i].to] + 1 && node[i].capa > 0) {
			ll wei = dfs(node[i].to, min(flow - used, node[i].capa));
			if (wei) {
				node[i].capa -= wei;
				node[i ^ 1].capa += wei;
				used += wei;
			}
		}
		if (used == flow)return used;
	}
	if (used > flow)used = flow;
	if (used < flow) {
		--gap[dep[u]];
		if (!gap[dep[u]])dep[s] = n + 1;
      ++gap[++dep[u]];
	}
        //这里的 if 语句才是与 Dinic 算法真正的不同之处
	return used;
}

你大概听说过一个与 ISAP 几乎一致的算法：“Dinic 算法”。

Dinic 算法与 ISAP 算法有一点不一样： Dinic 在 DFS 后直接暴力 BFS 维护层次图，但是 ISAP 却在 DFS 的时候也在维护层次图。这一点不同导致 ISAP 算法的运行速度往往比 Dinic 算法快上数倍。

ISAP 算法是这样维护层次图的：如果从上一个结点传过来的流量大于从这个结点增广出去的流量，那么将这个结点的深度 +$1$。

就是这么简洁。

你可能还想问：“为什么 ‘当增广后 $used$ 小于 $flow$ 时将结点 $u$ 的深度 +$1$’ 呢？”

请看：

if (used < flow) {
		--gap[dep[u]];
		if (!gap[dep[u]])dep[s] = n + 1;
     		++gap[++dep[u]];
	}

ISAP 的思想在这短短的几行代码里表现得淋漓尽致。

为什么这是对的？

假设有一个结点 $u \in V$ 是当前 DFS 考虑的结点，并且我们知道汇点 $t$ 的深度是不变的，因为我们遇到了汇点 $t$ 就 return，而源点 $s$ 的深度是每轮必变的，因为初始源点 $s$ 的 $flow$ 是 $\infty$。

这可以推导出一个很重要的结论：“当前 DFS 找到的增广路径长度相等且都等于 $\operatorname{dep}(s)$”。

这意味着如果有一个结点 $u \in V$， 从 $u$ 增广出去的流量小于增广路径上最小边权的容量，也就意味着经过 $u$ 的所有长度等于 $\operatorname{dep}(s)$ 的增广路都已经被增广过了，而且通过这个结论我们也可以证明，所有长度小于 $\operatorname{dep}(s)$ 的增广路都已经被增广完了。

这时候将结点 $u$ 的深度提高，相当于通过结点 $u$ 的增广路径长度变长了，也就能增广其他比原本的增广路更长的增广路了。

结束条件， gap 优化以及当前弧优化

while (dep[s] < n) {
		sum += dfs(s, inf);
		memcpy(cur, head, (n + 1) * sizeof(int));
	}

这是运行 ISAP 的核心代码之一。

可以看到结束条件是 dep[s]<n 。

为什么呢？因为增广路最长只有 $n$，dep[s] 等于 $n$ 时增广路肯定都找完了。

那 gap 优化又是优化到那里了呢？

if (used < flow) {
		--gap[dep[u]];
		if (!gap[dep[u]])dep[s] = n + 1;
     		++gap[++dep[u]];
	}

无比的合理，当一个深度对应的结点数目为 $0$ 的时候，那么就会形成断层，也就找不到增广路了，找不到增广路就说明已经是最大流了。这里利用 dep[s]=n+1 还能使程序少一个特判。

程序还使用了一个优化：“当前弧优化”。

当前弧优化的核心在这里：

for (int i = cur[u]; i != -1; i=node[i].next) {
	cur[u] = i;
        ...
}

这里的作用是：当我们再次遍历到这个点时，前面的边肯定已经被增广完了，就没必要再走了，在这里进行一次剪枝，速度也极大提升。

ISAP 的正确性：

在图 $G=(V,E)$ 中，很显然源点 $s$ 的深度在每次 DFS 后都会提高，并且每次 DFS 都找的是最短增广路，如果一直没出现断层，定义函数 $\operatorname{dep}(U),U \in V$ 为结点 $U$ 的深度。 最多会跑 $V-\operatorname{dep}(s)$ 次增广路，可以证明，当 $\operatorname{dep}(s) ≥ V$ 时必定出现断层，也就不存在增广路径，因此 ISAP 算法找出的一定是最大流。

时间复杂度分析：

在图 $G=(V,E)$ 中，BFS 是 $\Theta(V+E)$ 的，几乎不影响总时间复杂度。显然，每次 DFS 后，源点 $s$ 到汇点 $t$ 的距离都会增加 $1$，最多进行 $V-\operatorname{dep}(s)$ 次 DFS，直观上看，$\operatorname{dep}(s)$ 比 $V$ 的阶小，因此共进行 $O(V)$ 次 DFS，每次构造出一个新的层次图，图上最多有 $O(E)$ 个增广路，寻找每个增广路的时间最多是 $O(V)$ 的，所以 ISAP 算法的时间复杂度上限为 $O(V^2E)$。

证毕。

ACcode

#include <bits/stdc++.h>
using namespace std;
#define inf 1000000000000000
#define V 50010
#define E 1000010
typedef long long int ll;
struct edge {
public:
	int to, next;
	ll capa;
};
int cnt = 0, head[V]; int n, m; vector<edge>node(E);
inline void add(int fir, int nxt, ll w) {
	node[cnt].to = nxt;
	node[cnt].capa = w;
	node[cnt].next = head[fir];
	head[fir] = cnt; ++cnt;
}
int s, t, deep[V], gap[V], cur[V]; queue<int>que; ll sum = 0;
inline void initing() {
	memset(deep, -1, V * sizeof(int));
	memcpy(cur, head, (n+1)*sizeof(int));
}
inline void bfs() {
	int fro, ito;
	que.push(t); deep[t] = 0; ++gap[deep[t]];
	while (!que.empty()) {
		fro = que.front(); que.pop();
		for (register int i = head[fro]; i != -1; i = node[i].next) {
			ito = node[i].to;
			if (deep[ito] == -1) {
				deep[ito] = deep[fro] + 1;
				que.push(ito);
				++gap[deep[ito]];
			}
		}
	}
}
ll dfs(int u, ll flow) {
	if (u == t || flow == 0)return flow; ll used = 0,wei=0;
	for (int i = cur[u]; i != -1; i = node[i].next) {
		cur[u] = i;
		if (deep[u] == deep[node[i].to] + 1 && node[i].capa > 0) {
			wei = dfs(node[i].to, min(flow - used, node[i].capa));
			if (wei) {
				node[i].capa -= wei;
				node[i ^ 1].capa += wei;
				used += wei;
			}
		}
		if (used == flow)return used;
	}
	if (used < flow) {
		--gap[deep[u]];
		if (!gap[deep[u]])deep[s] = n + 1;
		++gap[++deep[u]];
	}
	return used;
}
ll ISAP() {
	initing(); bfs();
	while (deep[s] < n) {
		sum += dfs(s, inf);
		memcpy(cur, head, (n+1) * sizeof(int));
	}
	return sum;
}
int main() {
	ios::sync_with_stdio(0);
	memset(head, -1, V*sizeof(int));
	cin >> n >> m >> s >> t;
	int f, n; ll w;
	for (register int i = 0; i < m; i++) {
		cin >> f >> n >> w;
		add(f, n, w);
		add(n, f, 0);
	}
	cout << ISAP();
	return 0;
}