自动搬运

查看原文

来自洛谷，原作者为

	szkzyc 退役了

搬运于2025-08-24 21:13:49，当前版本为作者最后更新于2021-08-09 15:05:17，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

芝士提示：此题需要用到图论的基本知识，若没有了解请先到更简单的题目学习后再来解决此题。

这道题是“最短树”的一道模板题，也被称作“最小生成树”。

而对于求解“最小生成树”问题，主要有两种通用的算法：Prim 算法（适合求解稠密图）与 kruskal 算法（适合求解稀疏图）。

虽然此题适合用 Kruskal 算法，不过 Prim 算法也是能做的。两者都是最小生成树中重要的知识点。

因此，我会给大家分别介绍这两种的原理与源代码，不过核心思想都是相同的——贪心。

首先，问题是要求在一个带权连通无向图中求出一颗最短树（最小生成树），使得这个树的权值和最小。让你输出这个最小值是多少。

首先，让我们来介绍 Prim 算法：

Prim 算法求最小生成树：

（本图片来源于网络，若侵权请私信我，核实立刻删除）

我们就拿上图举例（在上图中，用红线连接的边就是要舍去的边，黑线就是最终选择的边）。Prim 算法构造的方法是首先从起始点 $A$ 开始（Prim 算法遍历开始的起始点可以选择任意一点，结果不会发生变化。一般我们习惯从 $1$ 或 $A$ 号点开始），找到所有能与它连边的点后找到权值的最小值并相连。然后相连后再对被相连的那个点进行贪心连边（在本图中是点 $B$）......重复以上操作，当连边的次数正好等于点数减一的时候，终止遍历，结束算法。（易证明，当连边次数正好等于点数减一时，树的边权最小）

想要计算权值和也很简单，因为一旦连边后便不会再更改，所以在每一次更改后加上连边的权值即可。

那么算法已经基本讲解完毕，接下来上代码！（Prim 算法中我用的是链式前向星来存图，重点是讲解算法，我便不再细讲）

#include<bits/stdc++.h> //万能头文件 
#define ll long long
#define INF INT_MAX  //INF表示无限，指一个极大值。INT_MAX是一个表示int范围内最大值的常量。 

using namespace std;
const int M = 3005;
const int N = 2005;
int n, m, tot, ans;
int head[N], dist[N], vis[N]; 
struct node{ //链式前向星存图 
	int to, next;
	int w;
}edge[M << 1]; //位运算，同等于M*2 
void addedge(int x, int y, int z){ //链式前向星的加边操作 
	tot++;
	edge[tot].to = y;
	edge[tot].w = z;
	edge[tot].next = head[x];
	head[x] = tot;
	return ;
}
void Prim(){ //Prim算法 
	for(int i = head[1]; i; i = edge[i].next){ //判段是否有重边 
		dist[edge[i].to] = min(dist[edge[i].to], edge[i].w); 
	}
	int u = 1; //u表示当前遍历到的点 
	for(int i = 1; i < n; i++){ //循环n-1次，也就是连n-1条边 
		int minn = INF; //先给最小值附一个极大的初值（我选择的是int的上限，2147483647，其实1e9便足矣） 
		vis[u] = true; //给这个点的访问标记标为真 
		for(int j = 1; j <= n; j++){ //遍历n个点找到权值最小的点 
			if(!vis[j] && dist[j] < minn){ //如果小于当前最小值 且没有被访问过 
				u = j; //记录下标 
				minn = dist[j]; //更新最小值 
			}
		}
		ans += minn; //答案加上这条边的边权 
		for(int k = head[u]; k; k = edge[k].next){ //链式前向星的遍历方式，找到点u所相连的全部点 
			int v = edge[k].to; 
			if(dist[v] > edge[k].w && !vis[v]){ //如果当前点所连的最小权值大于当前的权值且这个点没有被访问过 
				dist[v] = edge[k].w; //更新 
			}
		} 
	}
	return ;
}
void Init(){ //初始化 
	for(int i = 1; i <= n; i++){
		dist[i] = INF; //初始化一个极大值 
	} 
	dist[1] = 0; //但点1要标0 
	return ;
}
int main(){
    cin >> n >> m;
    while(m--){
    	int x, y, z;
    	cin >> x >> y >> z;
    	addedge(x, y, z); //由于是无向图，所以要存两遍 
    	addedge(y, x, z); //同上，x-->y 与 y-->x 
	}
	Init(); //初始化 
	Prim(); //Prim算法求解 
	cout << ans << endl; //输出答案 
	return 0;
} 
//B3603 by szkzyc

耗时 7 毫秒。

Kruskal 算法求最小生成树

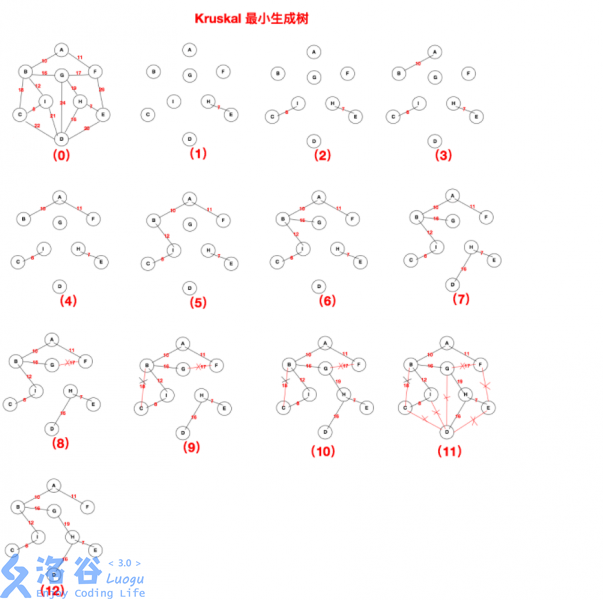
（来源于网络，侵私删）

然后我们来介绍 Kruskal 算法。

Kruskal的方法十分明了，算法过程中要运用到 并查集 不知道的同学可以点进这个链接看一下相关的例题。

我个人认为这个算法比 Prim 算法更加容易懂一些，就是将所有图之间的边权排序，然后从小到大的一个一个连。

会不会你认为这样就完了？不，还要判环。因为要构造的是最小生成树，不能出现环。如果出现了怎么办呢？简单，舍去后继续找就行了，直到连成了总点数减一的点就停止。

边权排序从小取比较简单，但判环就需要用并查集算法来判了。假设对于点 $x$ 与 $y$，利用并查集查找这两个点的祖先是否相同。如果相同便有环，不相同则无环。

Kruskal 算法的基本原理也已经明了，上代码！

#include<bits/stdc++.h>
#define ll long long
#define INF INT_MAX
using namespace std;
const int N = 2005;
const int M = 3005;
int ans = 0, sum = 0;
int n, m;
int fa[N]; //用来存储这个点的父节点 
struct node{
	int from, to, value;
}edge[M << 1]; 
bool cmp(node x, node y){ //定义排序函数 
	return x.value < y.value;
}
int find(int x){ //并查集，找到x的根节点 
	if(fa[x] != x) return fa[x] = find(fa[x]);
	return x;
}
void Kruskal(){ //Kruskal 
	int tot = 0;
	sort(edge + 1, edge + 1 + m, cmp); //将边权进行排序 
	for(int i = 1; i <= m; i++){
		int ft = find(edge[i].to);
		int ff = find(edge[i].from); //分别找到这两个点的根节点 
		if(ft != ff){ //如果不相同证明相连不会有环 
			tot++; //计数器加一 
			fa[ft] = ff; //将这两个点合并 
			ans += edge[i].value; //答案加上这个点的值 
		}
		if(tot == n) break; //如果进行了n次合并，那么退出循环，已经构造出最小生成树了。 
	}
}
int main(){
    cin >> n >> m;
    for(int i = 1; i <= n; i++) fa[i] = i; //最开始这个节点的父节点就是它自己 
    for(int i = 1; i <= m; i++){
    	cin >> edge[i].from >> edge[i].to >> edge[i].value; 
	} 
	Kruskal(); //进行Kruskal算法求解 
	cout << ans << endl; //输出答案 
	return 0;
}
//B3603 by szkzyc

耗时 3 毫秒。（在这道题中还是 Kruskal 算法有优势）

呼，终于讲完了，我们下次再见ヾ(￣▽￣)。Bye bye~~