自动搬运

查看原文

来自洛谷，原作者为

	zhn0707 Ciallo

搬运于2025-08-24 21:07:38，当前版本为作者最后更新于2021-07-09 11:44:36，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

题目大意

给你两个正整数 $X$ ， $Y$ ，求 $X$ ， $Y$ 之间有多少个素数。（$1 \leq X,Y \leq 10^5$）

题目分析 - 基础算法

我们先要了解以下东西：

1. 首先，素数和质数是一个东西。

2. 我们要知道素数指的是除了 $1$ 和它本身以外不再有其他因数的自然数。

简单点说，就是如果一个数是素数，那么它除了能整除 $1$ ，它本身之外，不能被其他数整除。

3. 最后，我们需要讨论一些特殊情况，如 $1$ 。（因为 $1$ 是和数）

4. 还有一点，原题中并没有说明 $X$ , $Y$ 谁大谁小，我们还要判断一下。

然后，在了解以上基本内容之后，我们想想看，是不是把 $X$ ， $Y$ 之间的所有数拿出来，然后依次检查，看它能不能满足上面的第二点条件。最后别忘了做一些特殊判断。

但是！！！

如果你以这个代码提交，就会得到这个结果：

（TLE表示超过时间限制）

为什么呢？可以猜想，可能是我们要用的时间太长了。因为题目数据范围直达$10^5$，而我们连套了两个循环。

那么怎么改善呢？

我们再引入一个概念：

若一个质数为 $n$ ，则它的两个因数，至少有其中一个 $\le \sqrt n$ 。

得到了这么个概念之后，我们就能缩小很大的范围。

另外，原代码中的一些点可以进一步优化。

最后，

个人认为如果你 for 循环写成 for(int j=1;j<=sqrt(i);j++) 因为要调出 <cmath> 头文件，就会麻烦，

因此建议写成 for(int j=1;j*j<=i;j++) 。

代码 - 基础算法（优化）

#include<iostream>
using namespace std;
int main(){
	int x,y,sum=0;
	bool jud=true;
	cin>>x>>y;
	if(x<y)swap(x,y);
	for(int i=x;i<=y;i++){//循环枚举所有情况 
		jud=true;
		if(i==1)continue;//判断 1 的特殊情况 ，就跳过本次循环 
		for(int j=2;j*j<=i;j++){//上文已提到的优化。注意是<=。 
			if(i%j==0){
				jud=false;//合数情况,标记false 
				break;//确认是合数，就直接退出，不用循环完 
			}
		}
		if(i==2)jud=true;
		if(jud==true)sum++;//是素数，计数器加一
	}
	cout<<sum;
	return 0;
}

---

如果你觉得这样就够了，那么你可以这篇题解就看到这里。

如果你想积累更多的且更好的筛选素数代码，请往下看。

---

题目分析 - 埃氏筛法

回忆一下，如果你还记得，（也许教材不一样，但接着往下看吧）小学的时候学习质数那一章的时候，有一张1~100的自然数表，课本是不是让你把 $2$ 的倍数划掉，然后是 $3$ 的倍数，然后 $5$ 的，$7$ 的……

很明显，这样筛选质数的方法肯定比所有都枚举一遍好得多。

下面放张动图祝你理解：

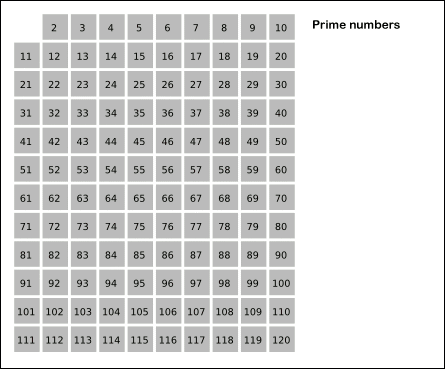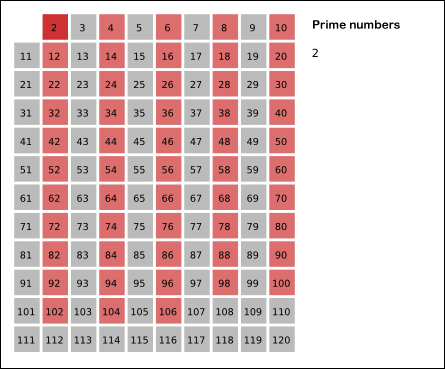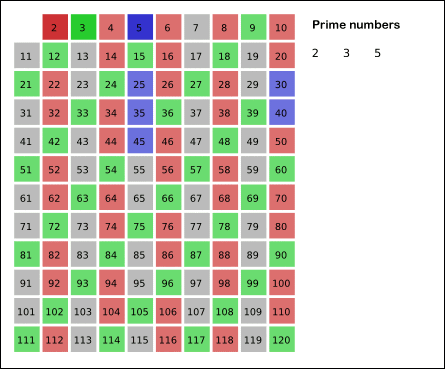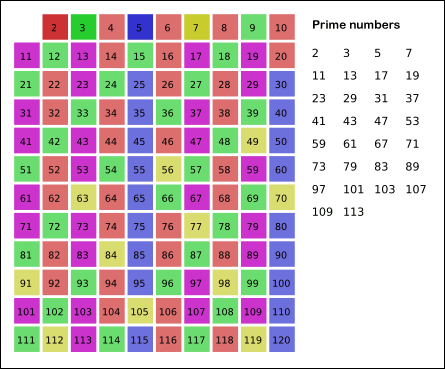
如果动图炸了，那看下面的视频吧：

点我

所以，我们首先假设所有数都是合数，然后再把 $2$ 的倍数等筛选出去。

然后，为了做这道题，把所有标记出来的素数计量一遍就好了。

代码 - 埃氏筛法

#include<iostream>
#include<cstring>
using namespace std;
int main(){
    int x,y,sum=0;
    bool is[1000001];
    cin>>x>>y;
    if(x>y)swap(x,y);//小的放前面
    memset(is,true,sizeof(is));//把所有的数都标记为素数。
    is[0]=is[1]=false;//特殊的两个素数
    for(int i=2;i<=y;i++)if(is[i])for(int j=2;j*i<=y;j++)is[j*i]=false;//有一种写法，是j<=y/i，但是C++除法有时候会出现一些玄学错误，建议能不用除法就不用除法
    for(int i=x;i<=y;i++)if(is[i])sum++;//记录
    cout<<sum;
    return 0;
}

P.S. 事实上，直接在定义的时候定义成 bool is[1000001]={} ，然后在下面的代码中写成 false 为素数， true 为合数即可。但编者为了让读者了解用 memset 的写法，故多写了 memset 一步。在“欧拉筛法”中，会写成前者的形式。

---

那么，还有更简的写法吗？

---

题目分析 - 欧拉筛法

让我们想一下，在筛选的时候，有一些数例如 $6$ ，在循环到 $2$ 、 $3$ 的时候是不是标记了两次？

那么，我们可不可以免掉这些操作，让判断的时候，不会出现重复呢？

事实上，可以。这时就要请出我们今天最后一位角色——欧拉筛法了。

其根本思想就是，限制限制使得合数在被检验时的方式唯一，不会重复检验。

由于最后一个比较难理解，所以放上模板代码和注释，请读者自行琢磨。

模板代码 - 欧拉筛法

int prime[1001]={},sum=0,n;//prime:存放素数 sum:素数数量 n:总数量 
bool is[1001]={1,1};
for(int i=2;i<=n;i++){
    if(!flag[i])prime[sum++]=i;//若是素数，加入数组 
    for(int j=0;i*prime[j]<=y;j++){
        flag[i*prime[j]]=true;//100%的合数 
        if(i%prime[j]==0)break;//避免重筛 
    }
}
cout<<sum;

---

感谢你看完。